- 真题试卷
- 模拟试卷
- 预测试卷
2. 设全集U=R,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知F1,F2为双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 定义在R上的函数f(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.△ABC的外接圆的圆心为O,半径为1,2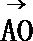
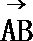
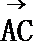
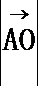
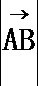
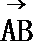
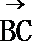
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 执行如图所示程序框图,输出结果S=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 如果数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.将函数f(x)=l+cos 2x-2sin2(x-
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设p:|4x-3|≤1,q: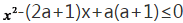
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 定义在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知两点


①
② 
③ 
④
其中为“和谐直线”的是______________(请写出符合题意的所有编号).
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
12.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.第1行:21+20
第2行:22+20,22+21
第3行:23+20,23+21,23+22
第4行:24+20,24+21,24+22,24+23
…
由上述规律,则第n行的所有数之和为______________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
(1)从这60名男生中按是否看营养说明采取分层抽样的方法,抽取一个容量为6的样本,问样本中看与不看营养说明的男生各有多少名?
(2)从(1)中的6名男生样本中随机选取2名作深度采访,求选到看与不看营养说明的男生各1名的概率;
(3)根据以上列联表,是否有85%的把握认为“性别与在购买食物时看营养说明”有关?
参考公式:

参考值表:
正确答案
解: (1)根据分层抽样可得:样本中看营养说明的男生有

(2)记样本中看营养说明的4名男生为
















其中符合要求的是







故所求的概率为
(3)假设

由题设条件得:
因为由

解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数f(x)=

(1)求函数f(x)在[0,π]上的单调递增区间和最小值;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,且fA.= -1,求
正确答案
由单调递增知:
解析
解析已在路上飞奔,马上就到!
知识点
18.如图, 





(1)求证:

(2)设点




正确答案
(1)证明:因为

所以
因为
所以
从而

(2)当M是BD的一个三等分点,即3BM=BD时,AM∥平面BEF.
取BE上的三等分点N,使3BN=BE,连结MN,NF,则DE∥MN,且DE=3MN,
因为AF∥DE,且DE=3AF,所以AF∥MN,且AF=MN,
故四边形AMNF是平行四边形.
所以AM∥FN,
因为AM

所以AM∥平面BEF.
解析
解析已在路上飞奔,马上就到!
知识点
19.设函数f(x)=x2 过点C(1,0)作x轴的垂线l1交函数f(x)图象于点A1,以A1为切点作函数f(x)图象的切线交x轴于点C2,,再过C2作x轴的垂线l2交函数f(x)图象于点 A2,…,以此类推得点An,记An的横坐标为an,n∈N*
(I) 证明数列{an}为等比数列并求出通项公式an;
(II) 设直线ln与函数g(x)= 

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,椭圆







(Ⅰ)若点


(Ⅱ)若椭圆



正确答案
(Ⅰ)
解:依题意,



所以 点

由点

所以 
解得 
(Ⅱ)解:设


因为 

所以 
因为 
所以 
由 ①,② 消去

所以 
当且仅当 
所以 

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)试判断函数

(2)当a=e,b=4时,求整数k的值,使得函数

(3)若存在

正确答案
解:(1)
由于



故函数

(2)


当




同理,




故当






故当



综上所述 

(3)
因为存在



①当




②当




③当

∴


∴当

而
设


∴


∴当

∴当

∴
∴
∴

设

∴函数

∴
即
解析
解析已在路上飞奔,马上就到!