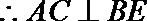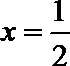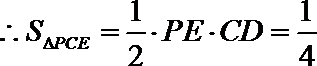文科数学 2013年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．已知集合，，且，则实数m的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

3．若，，，且，那么与的夹角为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

6．已知函数，是定义在R上的奇函数，当时，，则函数的大致图象为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

4．已知圆c与直线及都相切，圆心在直线上，则圆c的方程为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：单选题

分值: 5分

5．已知是等差数列，，，那么该数列的前13项和等于（）

A156

B132

C110

D100

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：单选题

分值: 5分

2．已知复数（），且有，是z的共轭复数，那么的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数的基本概念复数相等的充要条件复数代数形式的乘除运算

题型：单选题

分值: 5分

8．一个几何体的三视图如图所示，则该几何体的体积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

7．设变量x，y满足约束条件，则目标函数的最小值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求线性目标函数的最值

题型：单选题

分值: 5分

10．五张卡片上分别写有数字1，2，3，4，5，从这五张卡片中随机抽取2张，则取出的2张卡片上数字之和为奇数的概率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

9.定义在R上的偶函数f（x）满足，且在[-3，-2]上是减函数，α，β是钝角三角形的两个锐角，则下列结论正确的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11．抛物线的焦点坐标为________________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：填空题

分值: 5分

15．给出以下五个命题：

①命题“，”的否定是：“”；

②已知函数的图象经过点P（，1），则函数图象上过点P的切线斜率等于；

③是直线和直线垂直的充要条件；

④函数在区间（0，1）上存在零点；

⑤已知向量与向量的夹角为锐角，那么实数m的取值范围是（）。

其中正确命题的序号是________________。

正确答案

②③④

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：填空题

分值: 5分

12．已知x，y的值如下表所示：

如果y与x呈线性相关且回归直线方程为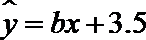，那么b=________________。

正确答案

0.5

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：填空题

分值: 5分

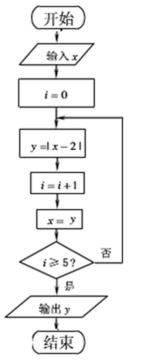
14．执行如图所示的程序框图，若输入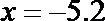，则输出y的值为________________。

正确答案

0.8

解析

解析已在路上飞奔，马上就到！

知识点

流程图的概念

题型：填空题

分值: 5分

13．某长方体的对角线长是4，有一条棱长为1，那么该长方体的最大体积为________________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱的结构特征棱柱、棱锥、棱台的体积

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 13分

16．已知，，若，求：

（1）的最小正周期及对称轴方程；

（2）的单调递增区间；

（3）当时，函数的值域。

正确答案

解：

（1）对称轴方程：

（2）增即为的减

（3）

值域为

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 12分

18．某省对省内养殖场“瘦肉精”使用情况进行检查，在全省的养殖场随机抽取M个养殖场的猪作为样本，得到M个养殖场“瘦肉精”检测阳性猪的头数，根据此数据作出了频率分布表和频率分布直方图如下：

（1）求出表中M，P以及图中a的值。

（2）若该省有这样规模的养殖场240个，试估计该省“瘦肉精”检测呈阳性的猪的头数在区间内的养殖场的个数。

（3）在所取样本中，出现“瘦肉精”呈阳性猪的头数不少于20头的养殖场中任选2个，求至多一个养殖场出现“瘦肉精”阳性猪头数在区间内的概率。

正确答案

（1）由知：

（2）养殖场有240个，分组[10，15]内的频率是0.25

估计全省在此区间内养殖场的个数为个

（3）设在区间内的养殖场为，在区间内的为

任选2个养殖场共，（），（），（），（），（），（），（），（），（），（），（），（），（），（）共15种情况，而两个养殖场都在区间内只有一种

故所求概率

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：简答题

分值: 12分

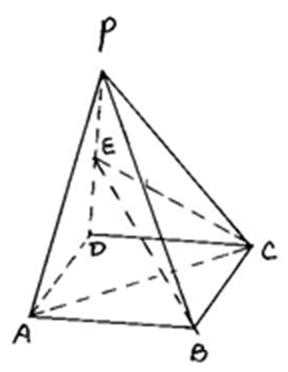
17．如图，四棱锥P-ABCD的底面是正方形，PD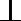面ABCD，E是PD上一点。

（1）求证：AC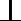BE。

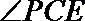
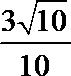
（2）若PD=AD=1，且的余弦值为，求三棱锥E-PBC的体积。

正确答案

解：（1）连接BD 是正方形

又面

面

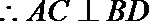
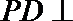
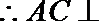
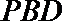
又BE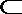面PBD；

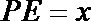
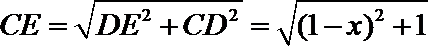
（2）设，则

又；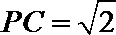

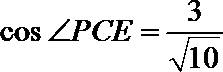
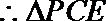
中，由余弦定理解为：

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积直线与直线垂直的判定与性质直线与平面垂直的判定与性质

题型：简答题

分值: 12分

19．设函数

（1）若函数在处取得极值-2，求a，b的值；

（2）若函数在区间（-1，1）内单调递增，求b的取值范围。

正确答案

（1）依题意：

（2）

当时

函数在（-1，1）内不可能增，舍去

当若时

递增

故所求范围为

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 13分

21．在平面直线坐标系XOY中，给定两点A（1，0），B（0，-2），点C满足，其中，且。

（1）求点C的轨迹方程；

（2）设点C的轨迹与双曲线（）相交于M，N两点，且以MN为直径的圆经过原点，求证：是定值；

（3）在（2）条件下，若双曲线的离心率不大于，求该双曲线实轴的取值范围。

正确答案

（1）设C（）则

（2）设M（）

N（）则，

韦达定理代入得

（定值）

（3）

又

代入得

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

题型：简答题

分值: 13分

20．已知数列的前n项和为，且满足各项为正数的数列中，对一切，有，且，，。

（1）求数列和的通项公式。

（2）设数列的前n项和为，求。

正确答案

（1）

时

当时

成等比数列

通项公式为：即：

又对一切 ……………………①

当时， ………………………②

①—②得

化简为

用换上式中n得：

两式相减整理得：即

数列为等差数列（当时）又

数列（成等差数列）

（2）错位相减得：

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式错位相减法求和

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷