- 真题试卷
- 模拟试卷
- 预测试卷
1.若
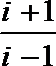
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.要得到函数y=cos2x的图象,只需将y=sin (2x+
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知非空集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在边长为1的菱形ABCD中,∠ABC=60O,将菱形沿对角线AC折起,使折起后BD=1,则三棱锥B-ACD的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是 边长为2的正方形,两条虚线互相垂直,则该几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知两点A (1,2), B (3,1) 到直线L的距离分别是
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知向量a=(x1,y1),b=(x2,y2),若|a|=2,|b|=3,a·b=-6,则的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 以双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 运行如图所示的程序框图,输出的结果是__________.
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
15. 若实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数列



正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
19.如图所示,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,Q是棱
(Ⅰ)若Q是PA的中点,求证:PC//平面BDQ;
(Ⅱ)若PB=PD,求证:BD⊥CQ;
(Ⅲ)在(Ⅱ)的条件下,若PA=PC,PB=3,
∠ABC=60º,求四棱锥P-ABCD的体积.
正确答案
(Ⅰ)连结AC,交BD于O.
因为 底面ABCD为菱形,
所以 O为AC中点.
因为 Q是PA的中点,
所以 OQ// PC,
因为OQ

所以PC//平面BDQ.
(Ⅱ)因为 底面ABCD为菱形,
所以 AC⊥BD,O为BD中点.
因为 PB=PD,
所以 PO⊥BD.
因为 PO∩BD =O,
所以 BD ⊥平面PAC.因为 CQ
所以 BD⊥CQ.
(Ⅲ)因为 PA=PC,
所以 △PAC为等腰三角形 .
因为 O为AC中点,
所以 PO⊥AC.
由(Ⅱ)知 PO⊥BD,且AC∩BD =O,
所以 PO⊥平面ABCD,即PO为四棱锥P-ABCD的高.
因为四边形是边长为2的菱形,且∠ABC=60º,
所以BO=
所以PO=
所以 
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数f(x)=2sin(ωx-

(1)求ω的值;
(2)在△ABC中,若A<B,且f(A)=f(B)=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
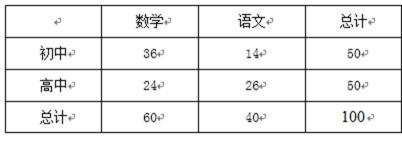
18.某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了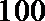
(Ⅰ) 用分层抽样的方法从喜欢数学的学生中随机抽取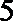
(Ⅱ) 在(Ⅰ)中抽取的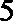
正确答案
(Ⅰ) 由表中数据可知, 高中学生应该抽取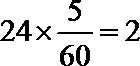
(Ⅱ) 记抽取的
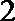
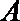
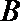
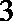

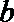
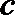
则从
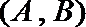
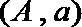
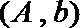
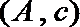
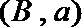
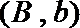
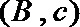
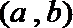
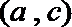
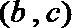
其中恰有1名高中学生的情况有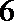
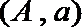
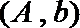
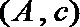
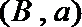
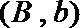
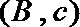
故所求概率为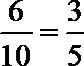
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆





(Ⅰ)求椭圆的方程;
(Ⅱ)若线段AB的中点的横坐标为

(Ⅲ)在


正确答案
(Ⅰ)∵椭圆离心率为

又



∴椭圆方程为

(Ⅱ) ∵直线L过点C(-1,0)且斜率为K,
则设直线方程为
由

若上式是与K无关的常数,则6m-1=0,∴
即在x轴上存在点M(

解析
解析已在路上飞奔,马上就到!
知识点
21.设

(Ⅰ)设a>0,若函数在区间
(Ⅱ)如果当x

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生在(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分. 请考生将所选题目后面的小矩形框涂黑。
22.选修4-1:几何证明选讲
如图,已知PA是



(1)求
(2)求AE的长.
23.选修4-4:坐标系与参数方程
已知圆


(1)把圆

(2)求经过两圆交点的直线的极坐标方程。
24.选修4-5:不等式选讲
已知不等式
(1)求实数m的取值范围;
(2)在(1)的条件下,当实数m取得最大值时,试判断
正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!