- 真题试卷
- 模拟试卷
- 预测试卷
3.已知关于





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在△ABC所在平面上有三点P、Q、R,满足


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知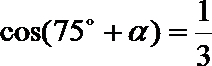
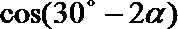
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若正数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 抛物线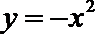
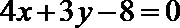
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数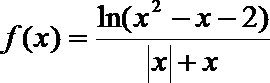
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
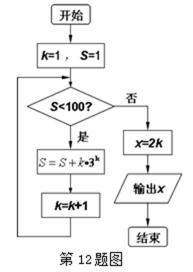
12.某程序框图如下图所示,该程序运行后输出的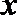
正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
13.一个几何体的三视图如图所示,其中正视图中
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 定义在





正确答案
-2013
解析
解析已在路上飞奔,马上就到!
知识点
15. 角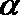
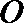
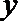
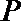
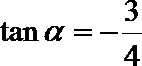
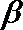
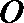
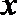
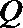
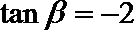
①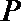
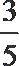
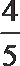
②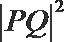
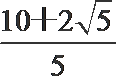
③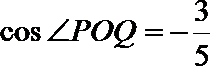
④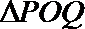
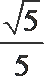
其中正确结论的编号是_____
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
17.随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
正确答案
解:(1)由茎叶图知:设样本中甲班10位同学的平均身高为

则




(2)设甲班的样本方差为



(3)由茎叶图可知:
乙班这10名同学中身高不低于173cm的同学有5人,
身高分别为173cm、176cm、178cm、179cm、181cm.
这5名同学分别用字母A、B、C、D、E表示.
则记“随机抽取两名身高不低于173cm的同学”为事件Ω,则Ω包含的基本事件有:
[A,B]、[A,C]、[A,D]、[A,E]、[B,C]、[B,D]、[B,E]、[C,D]、[C,E]、[D,E]
共10个基本事件.
记“身高为176cm的同学被抽中”为事件M,
则M包含的基本事件为:[A,B]、[B,C]、[B,D]、[B,E]共4个基本事件.
由古典概型的概率计算公式可得:
解析
解析已在路上飞奔,马上就到!
知识点
19.设数列





(1)求证:数列
(2)设直线









正确答案
解:(1)由题可知:


两式相减,得
又




故
(2)根据题意得:
两式相减得:
化简得:
解析
解析已在路上飞奔,马上就到!
知识点
16.在



(1)求
(2)求
正确答案
解:(1)由题可知:


由余弦定理可知


(2)由(1)知
则有

故
解析
解析已在路上飞奔,马上就到!
知识点
18.(如图,三棱柱ABC﹣A1B1C1的底面是边长为3的正三角形,侧棱AA1垂直于底面ABC,AA1=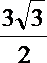
(1)求证:直线BC1∥平面AB1D;
(2)求三棱锥C1﹣ABB1的体积。
正确答案
(1)证明:由三棱柱ABC﹣A1B1C1可知:BC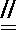
又D是CB延长线上一点,且BD=BC,故BD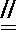
则四边形BDB1C1为平行四边形.故BC1∥DB1.
又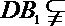
且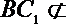
故BC1∥平面AB1D.
(2)由A点向BC作垂线,垂足记为E点,则AE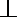
又AA1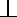
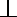
则CC1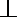
又ABC是边长为3的正三角形,故AE=
则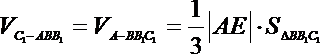
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆


(1)求椭圆
(2)过点




正确答案
解:(1)由题可知:椭圆的焦点在
又长轴的长为




故椭圆的标准方程为:
(2)由题可知:
①当


②当

设



则

联立


设

则
=
=
以


则
令


由二次函数的性质可得:

此时

综上可知:当


解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(Ⅰ)若

(Ⅱ)若



(Ⅲ)若

正确答案
解:(Ⅰ)因为
令


所以
(由


(Ⅱ)因为
因为


所以
只要
所以
(Ⅲ)因为

当


所以当

当



在
所以当

当



所以当

当


在


又
当


当


当



综上所述:
当

当

当



当



解析
解析已在路上飞奔,马上就到!