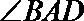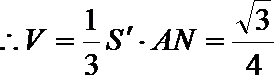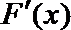- 真题试卷
- 模拟试卷
- 预测试卷
14.曲线

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
16.设V是已知平面M上所有向量的集合,对于映射








①设


②若




③对


④设




其中的真命题是( )(写出所有真命题的编号)
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
13.若点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知|



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(Ⅰ)求
(Ⅱ)设

正确答案
(Ⅰ)∵


(Ⅱ)∵









故
解析
解析已在路上飞奔,马上就到!
知识点
17.已知f (x)=
(1)求f (x)的定义域;
(2)判断f (x)的奇偶性并给予证明;
(3)求使f (x)>0的x的取值范围。
正确答案
解:(1) (–1,1)
(2) f (-x)=
∴函数y=f (x)是奇函数
(3) 若a>1, f (x)>0,则0<x<1
若0<a<1, , f (x)>0, 则-1<x<0
解析
解析已在路上飞奔,马上就到!
知识点
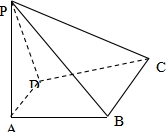
19. 如图,已知四棱锥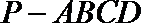
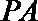

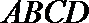
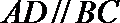

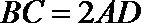
(1)求证: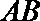
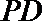
(2)在线段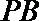
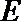
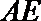
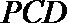
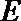
正确答案
(1)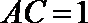
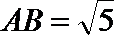
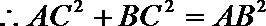
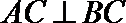
又∵平面PAC⊥平面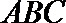
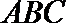
∴BC⊥平面PAC
又∵PA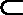
(2)取PC的中点N,连接AN,由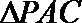
∴AN是四棱锥A—PCBM的高且AN= 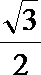
由BC⊥平面PAC,可知BC⊥PC,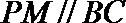
解析
解析已在路上飞奔,马上就到!
知识点
20.围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),
其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
正确答案
(Ⅰ)如图,设矩形的另一边长为a m,
则
由已知xa=360,得a=
(II)


即当x=24m时,修建围墙的总费用最小,最小总费用是10440元。
解析
解析已在路上飞奔,马上就到!
知识点
21.设数列






(Ⅰ) 求数列
(Ⅱ)是否存在实数


正确答案
(Ⅰ)由题意可得:



①─②得



(Ⅱ)解法一:
若
则
得
又


故存在实数

解法二:
欲使


故存在实数

解析
解析已在路上飞奔,马上就到!
知识点
22.已知定义在正实数集上的函数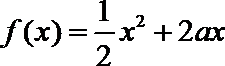
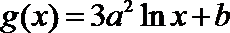
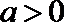
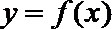
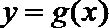
(I)用
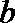
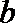
(II)求证: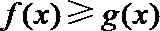
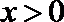
正确答案
(Ⅰ)设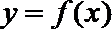
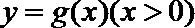
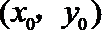
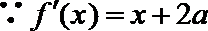
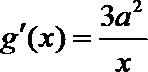
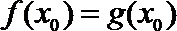
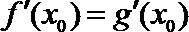
即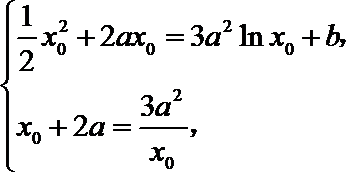
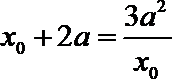
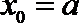
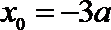
即有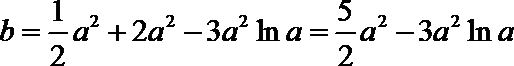
令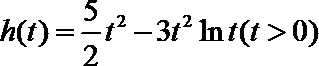
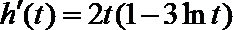
当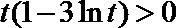
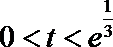
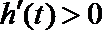
当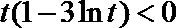
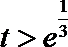
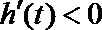
故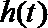
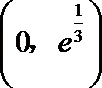
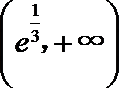
于是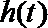
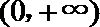
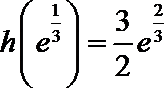
(Ⅱ)设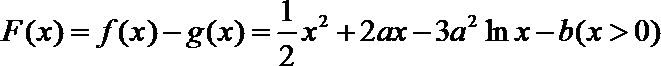
则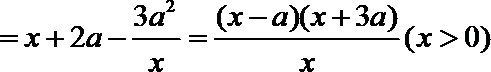
故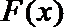
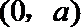
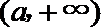
于是函数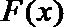
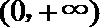
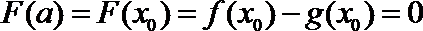
故当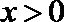
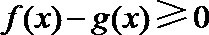
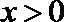
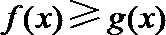
解析
解析已在路上飞奔,马上就到!
知识点
1.若复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.命题“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知向量







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在等差数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.记等比数列{an}的前n项和为Sn,若S3=2,S6=18,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数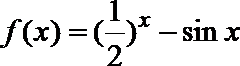
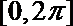
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知异面直线a、b分别在平面

正确答案
解析
解析已在路上飞奔,马上就到!
知识点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在正整数数列中,由1开始依次按如下规则将某些数染成红色.先染1,再染2个偶数2、4;再染4后面最邻近的3个连续奇数5、7、9;再染9后面最邻近的4个连续偶数10、12、14、16;再染16后面最邻近的5个连续奇数17、19、21、23、25.按此规则一直染下去,得到一红色子数列1,2,4,5,7,9,10,12,14,16,17,….则在这个红色子数列中,由1开始的第60个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知可导函数


正确答案
解析
解析已在路上飞奔,马上就到!