文科数学烟台市2014年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

3．设则的大小关系是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

4．“”是“函数为奇函数”的（）

A充分非必要条件

B必要非充分条件

C充要条件

D非充分非必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

6．在△ABC中，若则△ABC是 (　　 )

A等边三角形

B等腰三角形

C直角三角形

D既非等腰又非直角的三角形

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

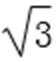
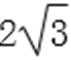
8．在△ABC中，内角A．B．C的对边分别是a．b．c，若a2－b2＝bc，sinC＝sinB，则A＝ (　　 )

A30°

B60°

C120°

D150°

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

10．已知函数满足条件，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

1．下列命题中是假命题的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

2．的零点所在区间为（）

A(0，1)

B(-1，0)

C(1，2)

D(-2，-1)

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

5．已知两座灯塔A．B与C的距离都是a，灯塔A在C的北偏东20°，灯塔B在C的南偏东40°，则灯塔A与灯塔B的距离为 (　　)

D2a

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

7．若满足条件C＝60°，AB＝，BC＝a的△ABC有两个，那么a的取值范围是(　 )

A（1，）

B(，)

C(，2)

D(1，2)

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

9．直线与曲线相切，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

11．函数的单调递增区间是（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化

题型：单选题

分值: 5分

12．某同学对函数进行研究后，得出以下结论：

①函数的图像是轴对称图形；

②对任意实数，均成立；

③函数的图像与直线有无穷多个公共点，且任意相邻两点的距离相等；

④当常数满足时，函数的图像与直线有且仅有一个公共点．

其中所有正确结论的序号是（）

A①②③

B③④

C①②④

D①④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

填空题本大题共4小题，每小题4分，共16分。把答案填写在题中横线上。

题型：填空题

分值: 4分

13．已知函数，若，那么__________

正确答案

-18

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

14．设α为△ABC的内角，且tanα＝，则sin2α的值为________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

分值: 4分

15．在等式的值为_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：填空题

分值: 4分

16．设向量，满足，，且与的方向相反，则的坐标为 _________。

正确答案

（-4，-2）

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

20．已知函数．

（1）求不等式的解集；

（2）设，其中R，求在区间[l，3]上的最小值．

正确答案

（1）

（2）

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

17．设命题p：函数的定义域为R；命题q：不等式，对∈(-∞，-1)上恒成立，如果命题“p∨q”为真命题，命题“p∧q”为假命题，求实数的取值范围．

正确答案

若真则∆<0且>0，故>2；

若真则，对x∈(-∞，-1)上恒成立，

在上是增函数，

此时x=-1，故≥1

“∨”为真命题，命题“∧”为假命题，

等价于，一真一假．故1≤≤2

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：简答题

分值: 12分

18．设函数f(x)＝cos ＋sin2x

（1）求函数f(x)的最大值和最小正周期；

（2）设A、B、C为△ABC的三个内角，若cosB＝，，且C为锐角，求sinA的值

正确答案

（1）

所以函数f(x)的最大值为最小正周期为π．

（2）

所以sinC＝，

因为C为锐角，所以C＝

在△ABC中，cosB＝，所以sinB＝

所以sinA＝sin(B＋C)＝sinBcosC＋cosBsinC

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

19．某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度：在C处进行该仪器的垂直弹射，观察点A．B两地相距100m，∠BAC＝60°，在A地听到弹射声音的时间比B地晚s．A地测得该仪器在C处时的俯角为15°，A地测得最高点H的仰角为30°，求该仪器的垂直弹射高度CH．(声音的传播速度为340m/s)

正确答案

由题意，设|AC|＝x，

则|BC|＝x－×340＝x－40，

在△ABC内，由余弦定理：

|BC|2＝|BA|2＋|CA|2－2|BA|·|CA|·cos∠BAC，

即(x－40)2＝x2＋10000－100x，

解得x＝420．

在△ACH中，|AC|＝420，

∠CAH＝30°＋15°＝45°，

∠CHA＝90°－30°＝60°，

由正弦定理：

可得

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 13分

22．已知函数，

（1）求函数的单调区间；

（2）在区间内存在，使不等式成立，求的取值范围。

正确答案

（1）函数的定义域为，

当，

即时，

为单调递增函数；

当，

即时，

为单调递减函数；

所以，的单调递增区间是，

的单调递减区间是

（2）由不等式，得，

令，则

由题意可转化为：

在区间内，，

，

令，得

由表可知：

的极小值是且唯一，

所以。

因此，所求的取值范围是。

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 13分

21．已知函数f(x)＝Asin(ωx＋φ)(x∈R，ω>0，0<φ< )的部分图象如图所示．

（1）求函数f(x)的解析式；

（2）求函数g(x)＝f(x－)－f(x＋)的单调递增区间．

正确答案

（1）由题设图象知，

周期T＝2(－)＝π，所以ω＝＝2．

因为点(，0)在函数图象上，

所以Asin(2×＋φ)＝0，

即sin(＋φ)＝0．

又因为0<φ<，

所以

从而＋φ＝π，即φ＝．

又点(0，1)在函数图象上，

所以Asin＝1，得A＝2．

故函数f(x)的解析式为f(x)＝2sin(2x＋)．

（2）g(x)＝2sin[2(x－)＋]－2sin[2(x＋)＋]

＝2sin2x－2sin(2x＋)

＝2sin2x－2(sin2x＋cos2x)

＝sin2x－cos2x＝2sin(2x－)．

由2kπ－≤2x－≤2kπ＋，

得kπ－≤x≤kπ＋，k∈Z．

所以函数g(x)的单调递增区间是[kπ－，kπ＋]，k∈Z．

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷