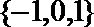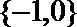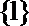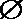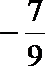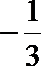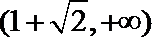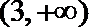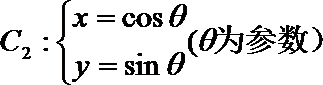- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合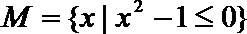
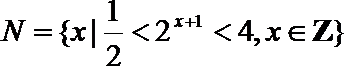
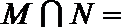
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.一个棱锥的三视图如图,则该棱锥的全面积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若定义在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若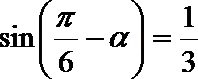
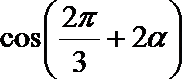
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设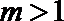
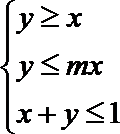
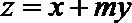
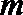
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.函数
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
16.已知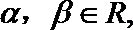
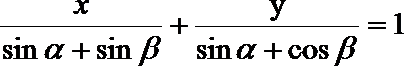
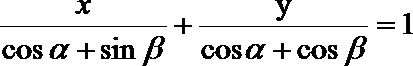

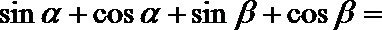
正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
15.


正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列
(Ⅰ)求数列
(Ⅱ)若



正确答案
解:(Ⅰ)


(1)-(2)得



解析
解析已在路上飞奔,马上就到!
知识点
18.有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份
















(Ⅰ)请你估计
(Ⅱ)如果把



正确答案
解:(Ⅰ)∵



方差




方差
∴ 
∴ 
(Ⅱ)从



其中样本








解析
解析已在路上飞奔,马上就到!
知识点
19.已知在四棱锥






(I)求平面

(II)若


正确答案
(I)证明:
∴
∵EF//CD,∴
∵

(II)解:∵CD//EF,∴CD//平面EFG,故CD上的点M到平面EFG的距离
等于D到平面EFG的距离,∴


∴D到平面EFG的距离即三角形EHD的高,等于
∴

解析
解析已在路上飞奔,马上就到!
知识点
20.已知离心率为






(Ⅰ)求椭圆方程;
(Ⅱ)过定点









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数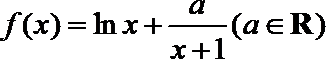
(1)当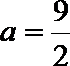
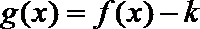
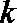
(2)当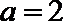
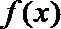
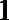
(3)求证: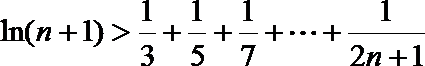
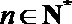
正确答案
解:(1)当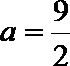
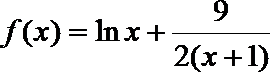
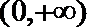
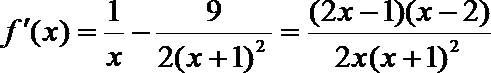
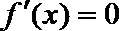
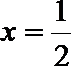
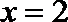
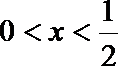
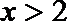
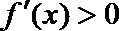
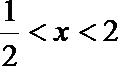
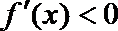
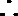
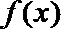
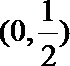
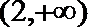
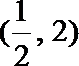
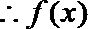
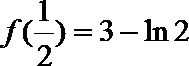
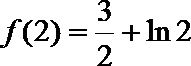
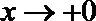
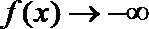
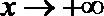
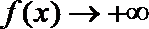
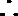
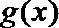
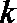
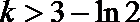
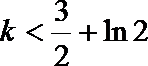
(3)(法一)根据(2)的结论,当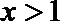
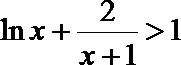
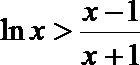
令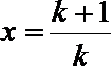
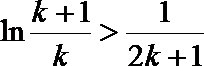
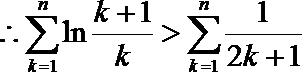
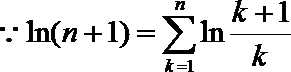
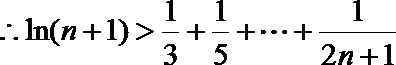
解析
解析已在路上飞奔,马上就到!
知识点
请考生在22、23、24三题中任选一题作答。
22.选修4-1:几何证明选讲
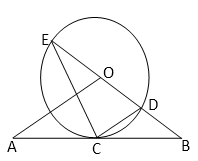
如图,直线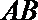
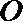
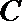
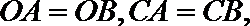
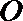
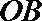
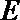
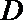
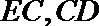
(I)求证:直线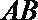
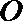
(II)若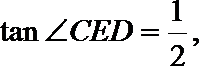
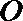
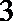
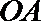
23.选修4-4:坐标系与参数方程
已知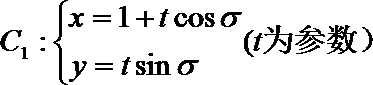
(I)当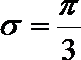
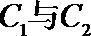
(II)过坐标原点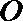
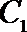
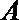
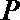
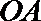
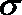
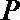
24.选修4-5:不等式选讲
已知函数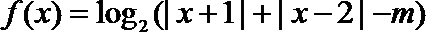
(I)当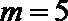
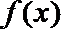
(II)若关于
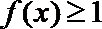
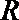
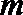

正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!