- 真题试卷
- 模拟试卷
- 预测试卷
2.下列命题错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.定义在R上的函数f(x)满足f(4)=1,



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.给出如图所示的程序框图,那么输出的数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知点P为双曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.将函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数
①定义域为实数集R;
②

③当x∈[-1,1]时,
则方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.曲线C1:(x-1)2+y2=1上的点到直线l:
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
12.如图,在△ABC中,已知AB=2,BC=3,



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知离心率为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.定义函数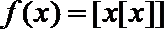
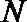
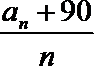
正确答案
13
解析
解析已在路上飞奔,马上就到!
知识点
15.已知以角B为钝角的


(I)求角B的大小;
(II)求sinA+cosC的取值范围.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知直三棱柱A1B1C1—ABC中,AC


(I)求证:BC1∥平面A1CD;
(II)求二面角A-A1C-D的余弦值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知F1、F2是椭圆

(1)求P点坐标;
(2)求证直线AB的斜率为定值;
(3)求△PAB面积的最大值,并求出此时直线AB的方程。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知a>0,函数
(I)当a=1时,求函数

(Ⅱ)求函数
(III)若在区间(0,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.一个盒子中装有5个编号依次为l、2、3、4、5的球,这5个球除号码外完全相同,有放回的连续抽取两次,每次任意地取出一个球.
(Ⅰ)用列举法列出所有可能结果;
(Ⅱ)求事件A=“取出球的号码之和不小于6”的概率;
(III)设第一次取出的球号码为x,第二次取出的球号码为Y,求事件B=“点(X,Y)落在直线y=x+1上方”的概率。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 设数列{an}的前n项和为Sn,对任意的正整数n,都有an =5Sn+1成立,记
(I)求数列{an}与数列{bn}的通项公式;
(Ⅱ)设数列{ bn }的前n项和为Rn,是否存存正整数k,使得Rn≥4k成立?若存在,找出一个正整数k;若不存在,请说明理由;
(III)记


正确答案
解析
解析已在路上飞奔,马上就到!






















































