文科数学淄博市2012年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

5．b2＝ac是a，b，c成等比数列的（）条件

A充分不必要

B必要不充分

C充要

D既不充分也不必要

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

7．将函数y=sin x的图象上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象的函数解析式是(　　)

Ay=sin(2x-)

By=sin(2x-)

Cy=sin(x-)

Dy=sin(x-)

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化

题型：单选题

分值: 5分

10．几何体的三视图如图所示，则这个几何体的直观图可以是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

1．若集合=（）

C[-1，0]

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

4．关于直线与平面，有以下四个命题：

①若且，则；

②若且，则；

③若且，则；

④若且，则；

其中真命题的序号是（）

A①②

B③④

C①④

D②③

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

6．抛物线的焦点坐标是（）

A(0，)

B(0， - )

C(0，)

D(0，- )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：单选题

分值: 5分

8．在数列{an}中，a1=2，an+1=an+ln(1+)，则an=（）

A2+ln n

B2+(n-1)ln n

C2+nln n

D1+n

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：单选题

分值: 5分

9．在区间上随机取一个数x，cosx的值介于0至之间在的概率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

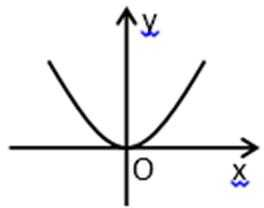
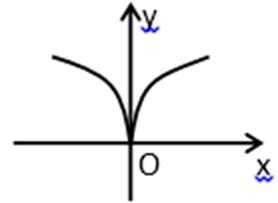
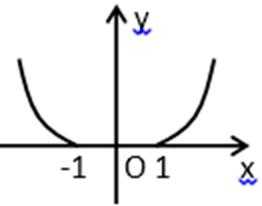
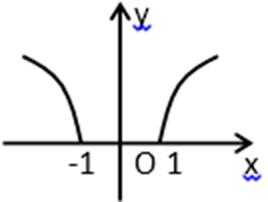
11．函数y=log(|x|+1)(a>1)的图象大致是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化

题型：单选题

分值: 5分

12．某加工厂用某原料由甲车间加工出A产品，由乙车间加工出B产品．甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品，每千克A产品获利40元．乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品，每千克B产品获利50元．甲、乙两车间每天共能完成至多70箱原料的加工，每天甲、乙车间耗费工时总和不得超过480小时，甲、乙两车间每天总获利最大的生产计划为（）

A甲车间加工原料10箱，乙车间加工原料60箱

B甲车间加工原料15箱，乙车间加工原料55箱

C甲车间加工原料18箱，乙车间加工原料50箱

D甲车间加工原料40箱，乙车间加工原料30箱

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

2．若复数为纯虚数，则实数的值是（）

A-1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

3．为了解某地高三学生的身体发育情况，抽查该地区100名年龄在17.5－18岁之间的男生体重(kg)得到频率分布直方图如下：

根据上图可得这100名学生中体重在[56.5，64.5]的学生人数是（）

A20人

B30人

C40人

D50人

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

填空题本大题共4小题，每小题4分，共16分。把答案填写在题中横线上。

题型：填空题

分值: 4分

16．设S为实数集R的非空子集，若对任意x，y∈S，都有x+y，x-y，xy∈S，则称S为封闭集，下列命题：

①集合S={a+b|a，b为整数}为封闭集；

②若S为封闭集，则一定有0∈S；

③封闭集一定是无限集；

④若S为封闭集，则满足S⊆T⊆R的任意集合T也是封闭集。

其中的真命题是___________ (写出所有真命题的序号)

正确答案

①②

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：填空题

分值: 4分

13．已知f(x)=+m是奇函数，则f(-1)的值是___________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

15．已知圆C1： (x＋1)2＋y2＝1和圆C2： (x－1)2＋y2＝25，则与C1外切而又与C2内切的动圆圆心P的轨迹方程是___________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：填空题

分值: 4分

14．执行如图的程序框图，如果输入的n是4，则输出的p是___________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

18．设平面向量=(m，1)， =(2，n)，其中m，n∈{1，2，3，4}

（1）请列出有序数组(m，n)的所有可能结果；

（2）若“使得⊥(－)成立的(m，n)”为事件A，求事件A发生的概率。

正确答案

（1）所有可能结果为

（2）因为，所以，

所以事件包含的结果有

共2种，所以

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：简答题

分值: 12分

19．如图，在直四棱柱中，已知，．

（1）求证：；

（2）设是上一点，试确定的位置，使平面，并说明理由．

正确答案

（1）连接，证明平面即可

（2）取中点，证明四边形为平行四边形即可

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

21．设函数，曲线在点（2，（2））处的切线方程为

（1）求的解析式；

（2）若对一切恒成立，求的取值范围；

（3）证明：曲线上任一点处的切线与直线和直线所围成的三角形面积为一值，并求此定值。

正确答案

（1）

（2）或

（3）6

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法

题型：简答题

分值: 12分

17．在△ABC 中，已知角A、B、C 所对的三条边分别是、、，且

（1）求证：；

（2）求函数的值域。

正确答案

（1）因为，

所以

（2），

因为

所以，

所以的值域为

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

分值: 12分

20．在数列中，，，．

（1）证明数列是等比数列；

（2）求数列的前项和；

（3）令，求数列的前项和。

正确答案

（1）首项为1，公比为4

（2）

（3）

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 14分

22．从椭圆(a>b>0)上一点M向x轴作垂线，恰好通过椭圆的左焦点F1，且它的长轴端点A及短轴端点B的连线AB平行于OM．

（I）求椭圆的离心率；

（II）若b=2，设Q是椭圆上任意一点，F2是右焦点，求△F1QF2的面积的最大值；

（III）当QF2AB时，延长QF2与椭圆交于另一点P，若△F1PQ的面积为20(Q是椭圆上的点)，求此椭圆的方程。

正确答案

（I），

因为，

所以，所以

所以

（II）

（III），设椭圆方程为，

与直线联立可得

．

所以，所以椭圆方程为．

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷