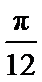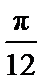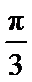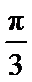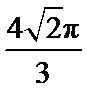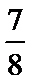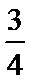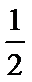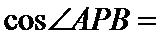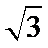2015年高考真题文科数学 (山东卷)

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1. 已知集合A={x| 2<x<4}, B={x| (x－1)(x－3)<0},则A∩B=( )

A. (1 , 3)

B. (1 , 4)

C. (2 , 3)

D(2 , 4)

正确答案

解析

因为B={x|1<x<3},所以A∩B=(2,3),故选C.

考查方向

集合交集及其运算，简单不等式的解法.

易错点

注意基本概念的正确理解以及基本运算方法的准确性.

知识点

交集及其运算

题型：单选题

分值: 5分

3. 设a=0.6，b=0.6,c=1.5,则a,b,c 的大小关系是（）

Aa<b<c

B a<c<b

Cb<a<c

D b<c<a

正确答案

解析

由y=0.6在区间（0，）是单调减函数可知，0<0.6<0.6<1,又1.5>1,故选C.

考查方向

指数函数的性质以及函数值比较大小.

解题思路

利用函数的单调性求解，需要结合指数函数底数的两种不同取值情况讨论.

易错点

指数函数的性质、指数函数底数的两种不同取值情况的讨论

知识点

等差数列的性质及应用

题型：单选题

分值: 5分

7. 在区间[0,2]上随机的取一个数x,则事件“－1”发生的概率为（）

正确答案

解析

由－1得，

，所以由几何概型概率的计算公式得，P=, 故选A.

考查方向

几何概型以及对数函数的性质.

解题思路

在理解几何概型概率计算方法的前提下，利用对数函数的单调性，求得事件发生的范围.

易错点

几何概型、对数函数的综合应用

知识点

随机事件的关系

题型：单选题

分值: 5分

2. 若复数z满足，其中i为虚数单位，则z=( )

A. 1－i

B. 1+i

C. －1－i

D. －1+i

正确答案

解析

由题意得=i(1－i)=1+i,所以，z=1－i,故选A.

考查方向

本题考查复数的概念和运算，共轭复数及其运算.

解题思路

采用分母实数化和利用共轭复数的概念进行化解求解.

易错点

分母实数化

知识点

复数代数形式的加减运算

题型：单选题

分值: 5分

4.要得到函数y=sin(4x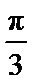－)的图象，只需要将函数y=sin4x的图象（）

A向左平移个单位

B向右平移个单位

C向左平移个单位

D向右平移个单位

正确答案

解析

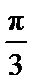
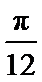
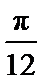
因为y=sin(4x－)=sin4(x－),所以，只需将函数y=sin4x的图象向右平移个单位，故选B.

考查方向

本题考查三角函数图象的变换。

解题思路

应用三角函数图象的变换规则分析求解。

易错点

明确平移的方向和单位数，取决于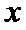加或减的数据.

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

分值: 5分

5. 设mR,命题“若m>0,则方程x+x－m=0有实根”的逆否命题是（）

A若方程x+x－m=0有实根，则m>0

B若方程x+x－m=0有实根,则m0

C若方程x+x－m=0没有实根，则m>0

D若方程x+x－m=0没有实根, 则m0

正确答案

解析

一个命题的逆否命题，要将原命题的条件、结论加以否定，并且加以互换，故选D

考查方向

命题的四种形式.

解题思路

明确命题的四种形式，正确理解“否定”的内容.

易错点

正确理解“否定”的内容.

知识点

充要条件的判定

题型：单选题

分值: 5分

8. 若函数是奇函数，则使成立的的取值范围为（）

A(－,－1)

B(－1，0)

C(0，1)

D(1，+)

正确答案

解析

由题意即所以,所以a=1,由得，则又因为则所以故选C.

考查方向

函数的奇偶性以及指数运算.

解题思路

利用函数的奇偶性，确定得到的取值，并进一步利用指数函数的单调性，求得的取值范围.

易错点

函数的奇偶性、指数函数的性质

知识点

幂函数图象及其与指数的关系

题型：单选题

分值: 5分

9.已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而

形成的曲面所围成的几何体的体积为（）

正确答案

解析

由题意知，该等腰直角三角形的斜边长为2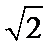，斜斜边上的高为，所得旋转体为同底等高的全等圆锥，所以其体积为，故选B.

考查方向

旋转体的几何特征以及几何体的体积，.在考查旋转体的几何特征及几何体的体积计算方法的同时，考查了考生的空间想象能力及运算能力，是“无图考图”的一道好题.

解题思路

理解所得旋转体的几何特征，确定得到计算体积所需要的几何量.

易错点

旋转体的几何特征的理解

知识点

余弦定理的应用

题型：单选题

分值: 5分

10. 设函数，若（）

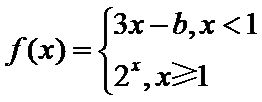
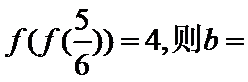
正确答案

解析

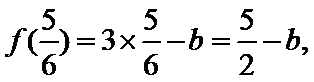
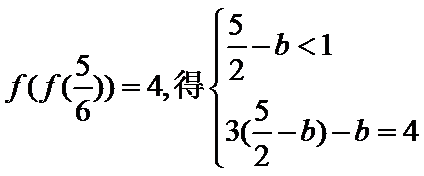
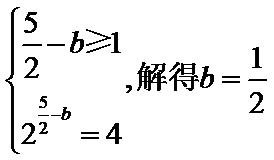
由题意，由或，故选D.

考查方向

分段函数以及函数与方程.

解题思路

理解分段函数的概念，明确函数值计算层次，准确地加以计算。

易错点

分段函数对应法则的选取与应用。

知识点

分式不等式的解法

题型：单选题

分值: 5分

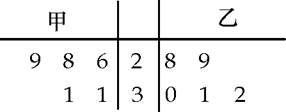
6. 为比较甲、乙两地某月14时的气温状况，随机选取该月中的5天，将这5天中14时的气温数据（单位：℃）制成如图所示的茎叶图。考虑以下结论：

第6题图

①甲地该月14时的平均气温低于乙地该月14时的平均气温;

②甲地该月14时的平均气温高于乙地该月14时的平均气温；

③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差；

④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差；

其中根据茎叶图能得到的统计结论的标号为（）

A①③

B①④

C②③

D②④

正确答案

解析

甲地数据为：26,28,29,31,31；乙地数据为：28,29,30,31,32；

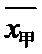
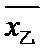
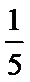
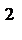
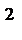
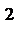
所以，==29，==30，

=[（26－29）+（28－29）+（29－29）+（31－29）+（31－29）] =3.6，

=[（28－30）+(29－30)+(30－30)+(31－30)+(32－30)]=2, 即正确的有①④，故选B.

考查方向

茎叶图，平均数，方差，标准差.

解题思路

结合茎叶图的概念以及平均数、方差、标准差的概念进行基本运算。

易错点

统计公式及概念的理解

知识点

茎叶图

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11. 执行右边的程序框图，若输入的x的值为1，则输出的y的值是.

第11题图

正确答案

解析

第一次执行程序，满足条件第二次执行程序，不满足条件结束答案为13.

考查方向

算法与程序框图.

解题思路

理解条件分支结构的基础上，准确地加以计算

易错点

对给定数据的验证分析，算法的理解

知识点

选择结构

题型：填空题

分值: 5分

12. 若满足约束条件则的最大值为____________.

正确答案

解析

画出可行域及直线平移直线当其经过点A(1，2)时，直线的纵截距最大，所以最大值为

第12题图

考查方向

简单线性规划.

解题思路

掌握线性规划的计算方法，准确做出可行域，应用线性目标函数的讨论方法求解

易错点

可行域的求作，目标函数的几何意义。

知识点

二元一次不等式（组）表示的平面区域

题型：填空题

分值: 5分

14.定义运算“”：R,)当的最小值是___________.

正确答案

解析

由新定义运算知，因为所以

，当且仅当

的最小值是

考查方向

新定义运算以及基本不等式.

解题思路

理解新定义运算，准确地得到不等式，然后根据其特征，想到应用基本不等式求解.

易错点

新定义运算问题的理解，基本不等式的条件

知识点

指数函数的图像变换

题型：填空题

分值: 5分

13. 过点P(1，)作圆的两条切线，切点分别为A,B则__________.

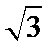
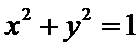
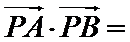
正确答案

解析

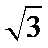
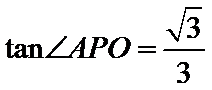
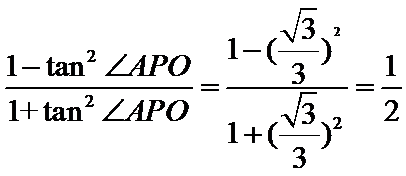
如图，连接PO,在直角三角形PAO中，OA=1,PA=,所以， ,

故 ==.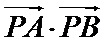

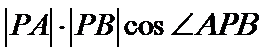
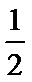
第13题图

考查方向

直线与圆的位置关系以及平面向量的数量积.

解题思路

结合图形特征，灵活地运用“几何方法”得到计算平面向量数量积的“要件”.

易错点

平面向量的数量积的定义，数形结合思想

知识点

二元二次方程表示圆的条件

题型：填空题

分值: 5分

15.过双曲线C:的右焦点作一条与其渐近线平行的直线，交C于点

P.若点P的横坐标为2a,则C的离心率为_______________.

正确答案

解析

双曲线的右焦点为（c,0）,不妨设所作直线与双曲线的渐近线平行，其方程为，代入,求得点P的横坐标为由得解得（舍去，因为离心率），故双曲线的离心率为2+.

考查方向

双曲线的几何性质与直线方程.

解题思路

首先是将问题进一步具体化，即确定所作直线与哪一条渐近线平行，事实上，由双曲线的对称性可知，两种情况下结果相同；其次就是能对所得数学式子准确地变形，利用函数方程思想，求得离心率.

易错点

直线、双曲线的几何性质，离心率的转化

知识点

双曲线的相关应用

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

18.角所对的边分别为.知cosB=.求sinA和c的值.

正确答案

c=1

解析

在

因为所以,因为所以C为锐角，cosC=，因此sinA=sin(B+C)=sinBcosC+cosBsinC=.

由可得，又ac=,所以c=1.

考查方向

考查两角和差的三角函数及正弦定理.

解题思路

应用两角和差的三角函数、正弦定理及函数方程思想，在正确理解题意的情况下，准确变形化简，从而得到计算结果。

易错点

忽视对角的范围的讨论，使解答陷入误区.

知识点

诱导公式的推导

题型：简答题

分值: 12分

如图，三棱台DEF－ABC中，AB=2DE, G, H 分别为AC,BC的中点.

19.求证：BD//平面FGH.

20.若CF求证：平面BCD⊥平面EGH.

第(1)小题正确答案及相关解析

正确答案

在三棱台DEF－ABC中，由BC=2EF,H为BC的中点，可得BH//EF,BH=EF,所以HBEF为平行四边形，可得BE//HF.在△ABC中，G,H分别为AC,BC的中点，所以GH//AB,又GHHF=H,所以平面FGH//平面ABED,因为BD平面ABED,所以BD//平面FGH.

解析

如图，连接DG,CD.设CDGF=M,连接MH,在三棱台DEF－ABC中，AB=2DE,G,H分别为AC,BC的中点，可得DF//CG,DF=CG,所以四边形DFCG是平行四边形，则M为CD的中点，所以HM//BD,又HM平面FGH,BD平面FGH,所以BD//平面FGH.

考查方向

考查线面平行的判定，应用线面平行的判定或者根据面面平行的性质。

解题思路

通过空间几何体的特征及空间直线与直线、直线与平面、平面与平面的平行关系，通过构造“面外一线与面内一线平行”或者构造两平面平行从而证明线面平行.

易错点

构造线面平行模型，辅助线或辅助面的做法

第(2)小题正确答案及相关解析

正确答案

(2) 证明：连接HE.因为G,H分别为AC,BC的中点，所以GH//AB,由ABBC,得GHBC,又H为BC的中点，所以EF//HC,EF=HC,因此四边形EFCH是平行四边形，所以CF//HE.又CFBC,所以HEBC.又HE,GH平面EGH,HEGH=H,所以BC平面EGH,又BC平面BCD,所以平面平面EGH.

解析

考查方向

考查面面垂直的判定，空间垂直关系的转化.

解题思路

通过空间几何体的特征及空间直线与直线、直线与平面、平面与平面的垂直关系的转化，在一面内寻找另一面的垂线，从而得证。

易错点

构造面面垂直模型，在一面内寻找另一面的垂线。

题型：简答题

分值: 13分

已知数列是首项为正数的等差数列，数列的前n项和为.

21.求数列的通项公式；

22.设.

第(1)小题正确答案及相关解析

正确答案

解析

（1）设数列的公差为d,令n=1,得所以令n=2,得

所以，解得，所以.

考查方向

考查等差数列的通项公式的求法

解题思路

运用从一般到特殊的处理方法，准确确定等差数列的通项公式。

第(2)小题正确答案及相关解析

正确答案

解析

(2)由（1）知，，所以

两式相减，

得，所以

考查方向

考查错位相减法求数列的前n项和，考查综合化简能力。

解题思路

对所得数学式子准确地变形，应用“错位相减法”求和。

易错点

错位相减后求和时，弄错数列的项数，或忘记从化简到.

题型：简答题

分值: 12分

某中学调查了某班全部45名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）

16.从该班随机选1名同学，求该同学至少参加上述一个社团的概率；

17.在既参加书法社团又参加演讲社团的8名同学中，有5名男同学,3名女同学现从这5名男同学和3名女同学中各随机选一人，求被选中且未被选中的概率.

第(1)小题正确答案及相关解析

正确答案

解析

（1）有调查数据可知，既未参加书法社团又未参加演讲社团的有30人，故至少参加上述一个社团的共有45－30=15人，所以从该班级随机选1名同学，该同学至少参加上述一个社团的概率为.

考查方向

考查随机事件的理解以及概率运算

解题思路

在正确理解题意的情况下，理解随机事件，通过比例解法求解。

易错点

随机事件的理解

第(2)小题正确答案及相关解析

正确答案

解析

(2)从这5名男同学和3名女同学中各随机选一人，其一切可能的结果组成的基本事件有

共15个.根据题意，这些基本事件的出现是等可能的.

事件“被选中且未被选中”所包含的基本事件有：,共2个.因此

被选中且未被选中的概率为.

考查方向

考查古典概型的基本事件的列举以及概率运算

解题思路

在正确理解题意的情况下，准确确定基本事件数，通过比例解法求解。

易错点

古典概型的基本事件的列举

题型：简答题

分值: 13分

设函数在点处的切线与直线平行.

23.求a的值；

24.是否存在自然数k,使得方程在（k,k+1）内存在唯一的根？如果存在，求出k;如果不存在，请说明理由；

25.设函数（min表示，p,q中的较小值），求m(x) 的最大值.

第(1)小题正确答案及相关解析

正确答案

解析

（1）由题意知，曲线y=f(x)在点（1,f(1)）处的切线斜率为2，所以又所以a=1.

考查方向

考查导数的几何意义；直线的位置关系

解题思路

利用导数的几何意义得到然后根据导数中的变量列方程求解。

易错点

导数的几何意义与切线斜率的关系。

第(2)小题正确答案及相关解析

正确答案

(2) k=1时，方程f(x)=g(x) 在(1,2)内存在唯一的根.设,当x(0,1时，h(x)<0.又h(2)=3ln2－所以存在.

因为,所以当x当x,所以当x（1，+）时，h(x)单调递增. k=1时，方程在（k,k+1）内存在唯一的根.

解析

见答案

考查方向

考查函数零点的存在性，利用导数研究函数零点。

解题思路

首先是通过构造函数，利用函数零点存在性定理，作出判断，并进一步证明函数在给定区间的单调性，明确方程在内存在唯一的根.

易错点

应用导数研究函数的性质、函数零点存在性定理。

第(3)小题正确答案及相关解析

正确答案

解析

(3)由（2）知，方程在（1,2）内存在唯一的根,且时，

,x(,+)时,,所以m(x)=,当x(0, )时，若x,m(x);若x，

由.

当x时，由，m(x)单调递增；x单调递减；可知m(x)综上可得函数m(x)的最大值为.

考查方向

考查利用导数研究函数的单调性、最值，考查转化与化归的思想。

解题思路

结合（2）的结论确定得到的表达式，并进一步利用分类讨论思想，应用导数研究函数的单调性、最值.

易错点

利用导数研究函数的单调性、最值.

题型：简答题

分值: 13分

平面直角坐标系中，已知椭圆C: 的离心率为且点,) 在椭圆C上.

26.求椭圆C的方程；

27.设椭圆E:,P为椭圆C上任意一点，过点P的直线交椭圆E于A,B两点，射线PO交椭圆E于点Q.

(i)求的值；

(ii)求面积的最大值.

第(1)小题正确答案及相关解析

正确答案

解析

（1）由题意知，解得.

所以椭圆的方程为.

考查方向

考查椭圆的标准方程及其几何性质；离心率的应用。

解题思路

将点的坐标代入椭圆方程结合离心率关系构造方程组求出系数a，b。

易错点

椭圆基本量的运算，几何性质中a，b，c三者关系。

第(2)小题正确答案及相关解析

正确答案

2，.

解析

（2）由（1）知椭圆E的方程为.

（i）设由题意知Q().根据.又

，即.

（ii）设A(),B(),将代入椭圆E的方程，可得由可得......①,则有.所以因为直线与轴交点的坐标为所以的面积.设将直线代入椭圆C的方程，可得

由可得……②

由①②可知0<t.故S.当且仅当t=1,即时取得最大值.由（i）知，的面积为3S,所以面积的最大值为.

考查方向

考查直线与椭圆的位置关系；距离与三角形面积；转化与化归思想.

解题思路

解答本题的主要困难是（II）中两小题，首先是通过研究的坐标关系，使（i）得解，同时为解答（ii）提供简化基础，即认识到与的面积关系，从而将问题转化成研究面积的最大值.通过联立直线方程、椭圆方程，并应用韦达定理确定“弦长”，进一步确定三角形面积表达式，对考生复杂式子的变形能力及逻辑思维能力要求较高.

易错点

转化与化归思想、三角形面积的化简求值与最值讨论

文科数学 热门试卷

正确答案

解析

考查方向

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

文科数学热门试卷