- 真题试卷
- 模拟试卷
- 预测试卷
1.集合
正确答案
解析
因为
所以
知识点
5.执行如图所示的程序框图,会输出一列数,则这个数列的第3项是( )
正确答案
解析
当N=1时,A=3,故数列的第1项为3,N=2,满足继续循环的条件,A=3×2=6;当N=2时,A=6,故数列的第2项为6,N=3,满足继续循环的条件,A=6×5=30;当N=3时,A=30,故数列的第3项为30,故选:B.
知识点
10.已知抛物线










正确答案
解析
设





知识点
2.
正确答案
解析
由已知得:



知识点
3.已知
正确答案
解析
略
知识点
6.已知定义在R上的函数f(x)满足(x+2)f′(x)<0,设
正确答案
解析
∵﹣2<

而(x+2)f′(x)<0,若x+2>0时,则f′(x)<0
所以函数f(x)在(﹣2,+∞)上是单调减函数,
∴f(ln3)<f(

∴c<b<a,
故选:B.
知识点
4.将函数


正确答案
解析
将函数



知识点
7.已知两座灯塔A、B与C的距离都是a,灯塔A在C的北偏东20°,灯塔B在C的南偏东40°,则灯塔A与灯塔B的距离为 ( )
正确答案
解析
略
知识点
8.若过点



正确答案
解析
由题意可设过点




知识点
9.抛物线






正确答案
解析
因为点A在抛物线上,所以有











知识点
11.已知双曲线中心在原点,一个焦点为



正确答案
解析
略
知识点
12.如果复数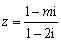
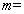
正确答案
-3
解析
略
知识点
14.已知向量a=(sin x,1),b=(t,x),若函数f(x)=a·b在区间上是增函数,则实数t的取值范围是__________.
正确答案
[-1,+∞)
解析
略
知识点
13.设函数


正确答案
解析
略
知识点
15.若集合







①集合

③设集合



④设集合



⑤对任意的一个“完美集”



其中正确结论的序号是 .
正确答案
②③④⑤
解析
①-1



②有理数集肯定满足“完美集”的定义;
③0




④对任意一个“完美集”A,任取








⑤



故答案为②③④⑤。
知识点
16.某市甲、乙两社区联合举行迎“五一”文艺汇演,甲、乙两社区各有跳舞、笛子演奏、唱歌三个表演项目,其中甲社区表演队中表演跳舞的有1人,表演笛子演奏的有2人,表演唱歌的有3人.
(1)若从甲、乙社区各选一个表演项目,求选出的两个表演项目相同的概率;
(2)若从甲社区表演队中选2人表演节目,求至少有一位表演笛子演奏的概率.
正确答案
(1)
(2)
解析
(1)记甲、乙两社区的表演项目:跳舞、笛子演奏、唱歌分别为A1,B1,C1;A2,B2,C2
则从甲、乙社区各选一个表演项目的基本事件有(A1,A2),(A1,B2),(A1,C2),(B1,A2),(B1,B2),(B1,C2),(C1,A2),(C1,B2),(C1,C2)共9种,
其中选出的两个表演项目相同的事件3种,所以
(2)记甲社区表演队中表演跳舞的、表演笛子演奏、表演唱歌的分别为a1,b1,b2,c1,c2,c3
则从甲社区表演队中选2人的基本事件有(a1,b1),(a1,b2),(a1,c1),(a1,c2),(a1,c3),(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),(c1,c2),(c1,c3),(c2,c3)共15种
其中至少有一位表演笛子演奏的事件有9种,所以
知识点
19.已知数列



(1)求数列

(2)设


正确答案
(1)
(2)
解析
(1)由
当

当n≥2时,









(2)由(1)得

由
得
∴
知识点
21.设函数

(1)对于任意实数


(2)若方程


正确答案
(1)4
(2)
解析
解析: (1)
对称轴
即
(2) 令




在区间
解得




在区间
解得
又∵




(Ⅳ) 当

综上:

知识点
20.在平面直角坐标系




(1)求椭圆
(2)










正确答案
(1)
(2)
解析
(1)设椭圆
由题意可得:
因此:椭圆
(2)⑴当



由题意可得:
将

所以:


又
因为


由①②得:



⑵当



由
设

此时:
所以
因为点

所以:

令
解得:



又
因为



将④代入⑤得:




综上所述:
知识点
17.已知向量
(1)当

(2)求

正确答案
(1)
(2)
解析
(1)

(2)
=




知识点
18.如图所示,在直三棱柱ABC-A1B1C1中, AC⊥BC.
(1) 求证:平面AB1C1⊥平面AC1;
(2) 若AB1⊥A1C,求线段AC与AA1长度之比;
(3) 若D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,试确定点E的位置;若不存在,请说明理由.
正确答案
见解析。
解析
(1)由于ABC-A1B1C1是直三棱柱,所以B1C1⊥CC1;
又因为AC⊥BC ,所以B1C1⊥A1C1,所以B1C1⊥平面AC1 .
由于B1C1
(2)由(1)知,B1C1⊥A1C .所以,若AB1⊥A1C,则可
得:A1C⊥平面AB1C1,从而A1C⊥ AC1 .
由于ACC1A1是矩形,故AC与AA1长度之比为1:1.
(3)点E位于AB的中点时,能使DE∥平面AB1C1.
证法一:设F是BB1的中点,连结DF、EF、DE.
则易证:平面DEF//平面AB1C1,从而
DE∥平面AB1C1.
证法二:设G是AB1的中点,连结EG,则易证EG
所以DE// C1G,DE∥平面AB1C1.





























































































