- 真题试卷
- 模拟试卷
- 预测试卷
2. 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.同时满足两个条件:①定义域内是减函数 ②定义域内是奇函数的函数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 等差数列







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设函数f(x)定义在实数集上,它的图象关于直线x=1对称,且当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7 .已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.如果sin


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知等比数列的公比为2,且前四项之和等于1,那么前八项之和等于_____________.
正确答案
17
解析
解析已在路上飞奔,马上就到!
知识点
14.函数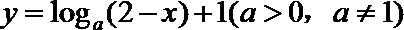
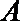

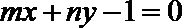
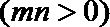

正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
16.在实数的原有运算中,我们补充定义新运算“






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若角


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.定义在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设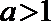
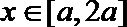
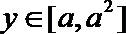
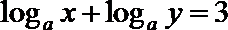
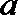
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知


(I)若不等式



(II)设全集


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设函数
(1)求函数
(2)当
正确答案
解:(1)

即

(2)当

所以
解析
解析已在路上飞奔,马上就到!
知识点
19.在数列


(1)设

(2)求数列

正确答案
解:(1)
即

(2)由(Ⅰ)
所以
解析
解析已在路上飞奔,马上就到!
知识点
22.若实数

(1)令

(2)若在区间



正确答案
(1)∵
∴
令

若



∴


当


∴

若





(2)若在


则



由(1)知,
当


∴此时

当



∴要满足条件应有函数

综上,实数


解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)若
(2)若
正确答案
(1)①
②
(2)当





根据条件,a应小于
同时a应大于

综上,a的取值范围是
解析
解析已在路上飞奔,马上就到!