- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合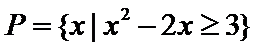
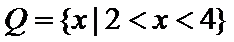
正确答案
解析
试题分析:由集合P={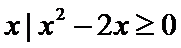
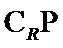
集即可。
P={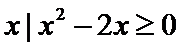
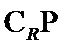
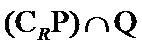
故选C.
考查方向
解题思路
首先由集合P中的元素满足的不等式求出集合P,然后求出集合P的补集,
最后求出集合P的补集与集合Q的交集.
易错点
求集合P的过程中不要忘了等号.
知识点
3.设a,b是实数,则“a+b>0”是“ab>0”的( )
正确答案
解析
试题分析:利用特值法进行判断。
a,b是实数,如果a=﹣1,b=2则“a+b>0”,则“ab>0”不成立.
如果a=﹣1,b=﹣2,ab>0,但是a+b>0不成立,
所以设a,b是实数,则“a+b>0”是“ab>0”的既不充分也不必要条件,故选D.
考查方向
解题思路
利用特例集合充要条件的判断方法,判断正确选项即可.
易错点
注意求充分或必要条件时的条件.
知识点
6.有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:

正确答案
解析
试题分析:利用作差法比较大小。
∵x<y<z且a<b<c,
∴ax+by+az﹣(az+by+cx)=a(x-z)+c(z-x)
=(x-z)(a-c)>0,
∴ax+by+cz>az+by+cx;
同理ay+bz+cx-(ay+bx+cz)=b(z-x)+c(x-z)
=(z-x)(b-c)<0,
∴ay+bz+cx<ay+bx+cz;
同理az+by+cx-(ay+bz+cx)
=a(z-y)+b(y-z)
=(z-y)(a-b)<0,
∴az+by+cx<ay+bz+cx,
∴最低费用为az+by+cx,故选B.
考查方向
解题思路
利用作差法逐个选项比较大小可得.
易错点
作差比较时要进行合理变形.
知识点
2.某几何体的三视图如图所示(单位:cm),则该几何体的体积是( 

正确答案
解析
试题分析:根据几何体的三视图确定几何体的形状,求出体积。
由三视图可知几何体是下部为棱长为2的正方形,上面是底面边长为2的正方形、
高为2的正四棱锥,∴几何体的体积为


考查方向
解题思路
判断集合体的形状,利用三视图的数据,求集合体的体积即可.
易错点
求棱锥的体积是不要忘记乘
知识点
4.设



正确答案
解析
试题分析:根据线面垂直,线面平行,面面平行的关系逐个进行判断。
对于A,∵l⊥



对于B,当



对于C,当l∥



对于D,当



考查方向
解题思路
A根据线面垂直的判定定理得出A正确;B根据面面垂直的性
质判断B错误C根据面面平行的判断定理得出C错误;D根据面面平行的性质判断D错误.
易错点
要考虑到空间直线,平面可能出现的各种关系.
知识点
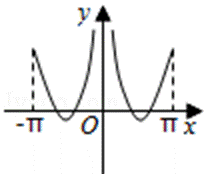
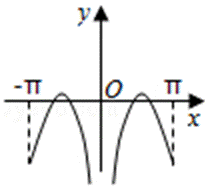
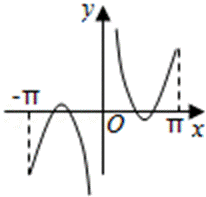
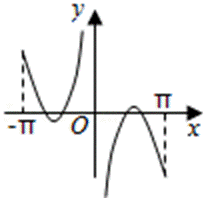
5.函数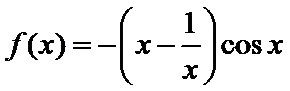
正确答案
解析
试题分析:根据函数的奇偶性判断出函数图象的对称性,利用0<x<1时函数值的正负进一步排除得出答案。
对于函数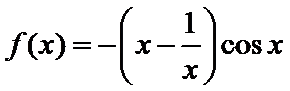
且满足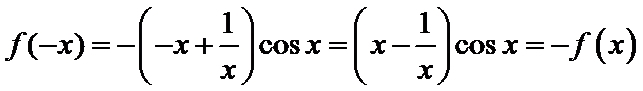
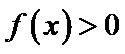
考查方向
解题思路
由条件可得函数f(x)为奇函数,故它的图象关于原点对称;再根据但是当x趋向于0时,f(x)>0,结合所给的选项,得出结论.
易错点
判断函数的奇偶性首先要看函数的定义域.
知识点
7.如图
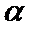
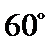
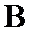
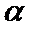
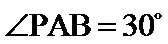
正确答案
解析
试题分析:用垂直于圆锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线.
此题中平面α上的动点P满足∠PAB=30°,可理解为P在以AB为轴的圆锥的侧面上,
再由斜线段AB与平面α所成的角为60°,可知P的轨迹符合圆锥曲线中椭圆定义.
故可知动点P的轨迹是椭圆。故选C.
考查方向
解题思路
根据题意,∠PAB=30°为定值,可得点P的轨迹为一以AB为轴线的圆锥侧面与平面α的交线,则答案可求.
易错点
正确理解空间角的关系.
知识点
8.设实数a,b,t满足|a+1|=|sinb|=t( )
正确答案
解析
试题分析:根据题中给出的条件确定a,b,t的关系,利用排除法找出答案。
∵实数a,b,t满足|a+1|=t,∴

t确定,则

∴若t确定,则
故选B.
考查方向
解题思路
根据代数式得出

易错点
利用已知条件找出a,b,t的关系.
知识点
11.函数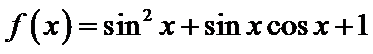

正确答案
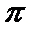
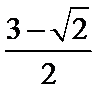
解析
试题分析:利用二倍角公式,两角差的正弦公式转化为一个角的三角函数,然后求出最小正周期和最小值。
∵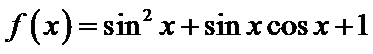

∴最小正周期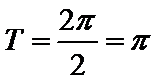
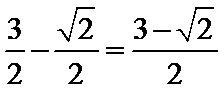
故答案为: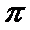
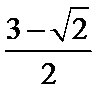
考查方向
解题思路
由三角函数恒等变换化简解析式可得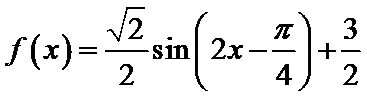
易错点
三角函数中三角公式的灵活应用.
知识点
10.已知





正确答案

解析
试题分析:利用题中给出条件求出首项和公差的关系,列方程求出值即可。
由


即



即

故答案为
考查方向
解题思路
运用等比数列的性质,结合等差数列的通项公式,计算可得
条件
易错点
注意等差数列和等比数列的性质的合理运用.
知识点
9.计算:

正确答案


解析
试题分析:根据对数的运算法则化简计算即可。


故答案为:

考查方向
解题思路
直接利用对数运算法则化简求值即可.
易错点
对数的运算法则的应用.
知识点
14.已知实数x,y满足
正确答案
15
解析
试题分析:由直线与圆的位置关系,去掉绝对值,利用线性规划求出最大值。
由

要使z=-3x-4y+10最大,则直线
由z=-3x-4y+10,得3x+4y+z-10=0.
则
故答案为:15.
考查方向
解题思路
由题意可得2x+y-4<0,6-x-3y>0,去绝对值后得到目标函数z=﹣3x﹣4y+10,然后结合圆心到直线的距离求得|2x+y-4|+|6-x-3y |的最大值.
易错点
根据直线与圆的位置关系来判断绝对值内数值的正负.
知识点
15.椭圆

正确答案
解析
试题分析:利用点F关于直线
设Q(m,n),由题意可得



可得,

可得

故答案为:
考查方向
解题思路
设出Q的坐标,利用对称知识,集合椭圆方程推出椭圆几何量之间的关系,然后求解离心率即可.
易错点
点关于直线的对称点的求法,.
知识点
12.已知函数


正确答案


解析
试题分析:利用分段函数的解析式求出函数值,求出分段函数每一段上的最小值,的导函数的最小值。
由题意可得

∵当x≤1时,
当x>1时,

当且仅当


∵

故答案为:

考查方向
解题思路
由分段函数的特点易得
易错点
分段函数求函数值注意代入到对应的解析式中,利用基本不等式求最值注意等号成立的条件.
知识点
13.已知




正确答案

解析
试题分析:根据向量数量积的定义求出向量的夹角,再利用题中给出的条件求出
∵











故答案为:
考查方向
解题思路
根据数量积得出

易错点
向量数量积的公式的应用.
知识点
16.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知
(1)求
(2)若
正确答案
(1)
解析
试题分析:(1)利用两角和的正切公式及同角三角函数关系式求解;(2)求出角A的正弦值和余弦值,利用正弦定理求出b,再利用诱导公式和两角和的正弦求出sinC,最后求三角形的面积
(1)由


所以

(2)由

又由


由sinC=sin(A+B)=

设△ABC的面积为S,则
考查方向
解题思路
(1)由两角和与差的正切函数公式及已知可得tanA,由倍角公式及同角三角函数关系式即可得解.
(2)由

易错点
同角三角函数关系,诱导公式的应用.
知识点
17.已知数列



(1)求

(2)记数列


正确答案
(1)


解析
试题分析:(1)利用等比数列的通项公式求出


(2)利用错位相减法求和即可。
(1) 由


∵


当n≥2时,

即

(2)由(1)可得
∴

∴
考查方向
解题思路
(1)直接由








(2)求出


易错点
错位相减法求和时的计算,分类讨论的思想的应用.
知识点
22.(本题满分15分)设函数
(1)当

(2)已知函数
正确答案
(1) 

解析
试题分析:(1)利用函数解析式求出二次函数的对称轴,分类讨论求出函数的最小值;(2)设出方程
(1)当


当a≤﹣2时,函数f(x)在[﹣1,1]上递减,则
当﹣2<a≤2时,即有

当a>2时,函数f(x)在[﹣1,1]上递增,则
综上可得,
(2)设s,t是方程

由于0≤b-2a≤1,
由此
当0≤t≤1时,
由

得

当﹣1≤t<0时,
由


故b的取值范围是
考查方向
解题思路
(1)求出二次函数的对称轴方程,讨论对称轴和区间[﹣1,1]的关系,运用函数的单调性即可得到最小值;
(2)设s,t是方程
易错点
根据二次函数的对称轴求函数在闭区间上的单调性,基本不等式求最值时灵活变形.
知识点
如图,在三棱锥




18.证明: 

19.求直线


正确答案
详见解析;
解析
利用线面垂直的判定定理证得结论成立;
证明:∵AB=AC=2,D是
∴
∵BC∥
∴
∵

∴
∵BC∩AO=O,
∴

考查方向
解题思路
连接AO,

易错点
空间向量的计算.
正确答案

解析
建立坐标系如图
∵在三棱柱

∴O(0,0,0),B(0,

即


设平面



得出

∴
可得出直线



考查方向
解题思路
利用空间向量的垂直得出平面





易错点
空间向量的计算.
如图,已知抛物线





注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则该直线与抛物线相切,称该公共点为切点.
20.求点A,B的坐标;
21.求△PAB的面积.
正确答案


解析
试题分析:(1)利用点斜式方程,直线与抛物线相切,求出点A坐标;利用点关于直线对称点的求法得到点B的坐标;由直线PA的斜率存在,设切线PA的方程为:y=k(x﹣t)(k≠0),联立

∵
∴x=2t,∴
圆

∴

∴
考查方向
解题思路
由直线PA的斜率存在,设切线PA的方程为:y=k(x﹣t)(k≠0),与抛物线方程联立,利用△=0,解得k=t,可得A坐标.圆

易错点
点关于直线对称点的计算,直线与圆锥曲线方程联立的计算.
正确答案

解析
利用两点间距离公式公式和点到直线的距离公式求出三角形的底边长和高,求出三角形面积。
由(1)可得:

∴点P到直线AB的距离
又
∴
考查方向
解题思路
由(1)可得AB方程:

易错点
点关于直线对称点的计算,直线与圆锥曲线方程联立的计算.