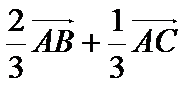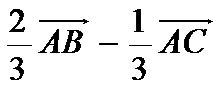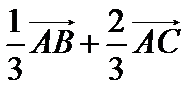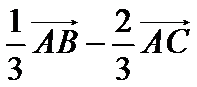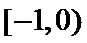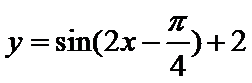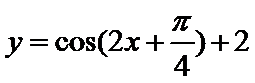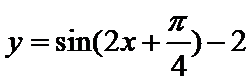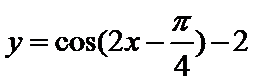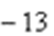- 真题试卷
- 模拟试卷
- 预测试卷
7.若△


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
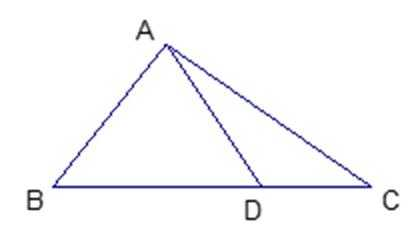
8.如图,在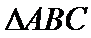
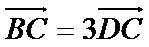
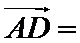
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知向量a



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知方程



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合A={x|-1≤x≤2},B={x|x2-4x>0,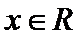
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 在数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知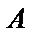

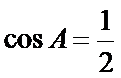
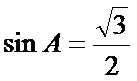
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.将函数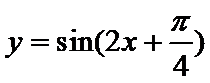
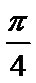
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在同一坐标系中画出函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知正项组成的等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知函数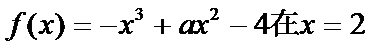

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 设单位向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.①

②函数
③已知函数




④


上述命题中是真命题的有________。
正确答案
②③④
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列








(Ⅰ) 求数列


(Ⅱ)设


正确答案
解:(Ⅰ)∵


∴ 




再由
∴

∴
(Ⅱ)


解析
解析已在路上飞奔,马上就到!
知识点
18.已知向量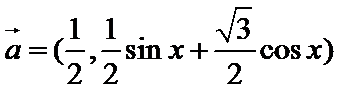
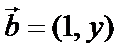
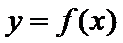
(1)求函数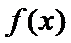
(2)已知锐角 △ABC 中的三个内角分别为 A、B、C,若有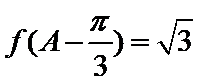
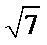
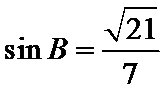
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图是三棱柱


(1)求证:
(2)设



正确答案
(1)由三视图画出直观图,如图,
这是一个正三棱柱,连接





因为

(2)过



因为侧面垂直于底面,所以



由
故,表面积为

解析
解析已在路上飞奔,马上就到!
知识点
从下列题中选答1题。
22.(几何证明选讲)
如图,AD是⊙O的直径,AB是⊙O的切线,M, N是圆上两点,直线MN交AD的延长线于点C,交⊙O的切线于B,BM=MN=NC=1,求AB的长和⊙O的半径.
23.(极坐标和参数方程)
以直角坐标系原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线l的参数方程为

(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于A、B两点,当α变化时,求|AB|的最小值.
24.(不等式选讲)
设函数





正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)当

(2)若对于任意


(3)若过点


正确答案
(2)方法1:由

因为对于任意

即对于任意

即对于任意

令
要使对任意

必须满足
即
所以实数

(3)设点

则过点

所以过点

因为点

即
若过点

则方程
令


令


因为

所以必须

所以实数

解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆


(1)求椭圆的方程;
(2)若过点C(-1,0)且斜率为







正确答案
解: (1)∵椭圆离心率为
又

所以
∴椭圆方程为

(2)在x轴上存在点M

假设在x轴上存在点M(m,0),使
∵直线L过点C(-1,0)且斜率为K,∴L方程为
由
设
∵
∴
设常数为t,则
整理得


即在x轴上存在点M(

解析
解析已在路上飞奔,马上就到!