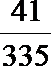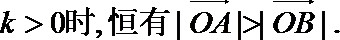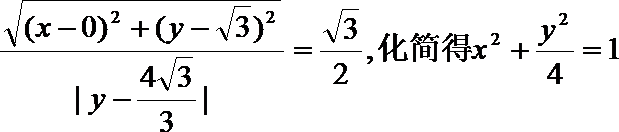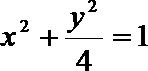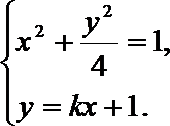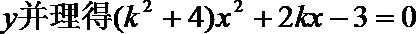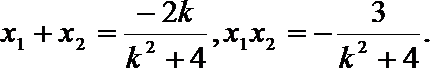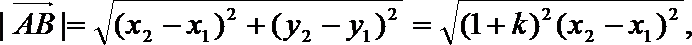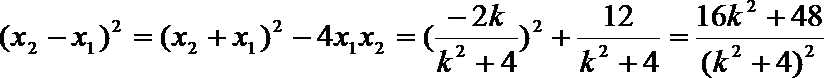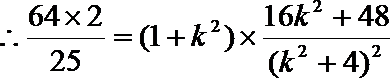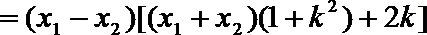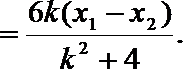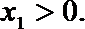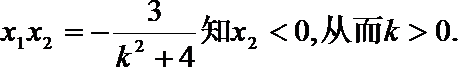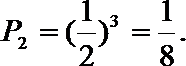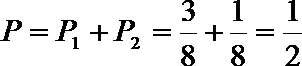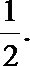文科数学兰州市2010年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

6．函数的单调递增区间是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

9．已知设是非零向量，若函数且，则函数的图像是（）

A过原点的一条直线

B不过原点的一条直线

C对称轴为轴的抛物线

D对称轴不是轴的抛物线

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

3．函数的最大值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

5．平面α的斜线AB交α于点B，过定点A的动直线与AB垂直，且交α于点C，则动点C的轨迹是（）

A一条直线

B圆

C椭圆

D双曲线的一支

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：单选题

分值: 5分

10．已知是等差数列的前n项和，若，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

题型：单选题

分值: 5分

1．已知集合为（）

A{1，2，3，4}

B{1，3，4，5}

C{2，3，4，5}

D{1，2，3，4，5}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

交、并、补集的混合运算

题型：单选题

分值: 5分

2．某中学高一年级有560人，高二年级有540人，高三年级有520人，用分层抽样的方法抽取容量为81的样本，则在高一、高二、高三三个年级依次抽取的人数分别是（）

A28、27、26

B28、 2 6、2 4

C26、27、28

D27、 26、25

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

分层抽样方法

题型：单选题

分值: 5分

4．已知函数的导函数，命题处取得极值，则的（）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分又不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定导数的几何意义利用导数求函数的极值

题型：单选题

分值: 5分

7．下列结论正确的是（）

A当

B当

C当的最小值是2

D当无最大值

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

8．在正方体ABCD—A1B1C1D1中，E、F分别是棱CC1与D1C1的中点，则直线EF与A1C1所成角正弦值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

11．已知直线与两坐标轴分别相交于A、B两点，圆C的圆心的坐标原点，且与线段AB有两个不同交点，则圆C的半径的取值范围是（）

D（3，4）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：单选题

分值: 5分

12．从数字0，1，2，3，5，7，8，11中任取3个分别作为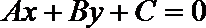中的A，B，C（A，B，C互不相等）的值，所得直线恰好经过原点的概率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

古典概型的概率

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

16．设______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等差数列的基本运算等比数列的判断与证明数列与函数的综合

题型：填空题

分值: 5分

15．已知点P、Q是内的点，O为坐标原点，则的取值范围是_____。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：填空题

分值: 5分

13．已知曲线平行，则实数 _____。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

题型：填空题

分值: 5分

14．已知则的值是______。（用数字作答）

正确答案

-243

解析

解析已在路上飞奔，马上就到！

知识点

平行关系的综合应用

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

20．已知数列是首项为3，公差为2的等差数列，其前为等比数列，且是公比为64的等比数列。

（I）求的通项公式；

（II）求证：

正确答案

解：（I）依题意有：

设

是公比为64的等比数列

（II）

…

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 12分

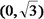
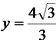
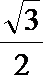
22．在平面直角坐标系xoy中，动点P到定点距离与到定直线：的距离之比为，设动点P的轨迹为C。

（I）写出C的方程；

（II）设直线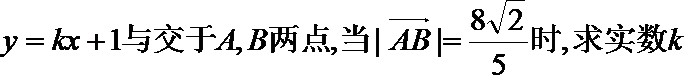的值。

（III）若点A在第一象限，证明：当

正确答案

解：（I）设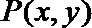，则依题意有：

故曲线C的方程为

注：若直接用

得出，。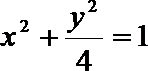

（II）设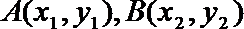，其坐标满足

消去

故

而

化简整理得

解得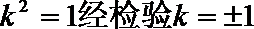：时方程※的△>0

（III）

因为A在第一象限，故

由

故

即在题设条件下，恒有

解析

解析已在路上飞奔，马上就到！

知识点

圆的标准方程

题型：简答题

分值: 10分

17．已知函数的最小正周期为

（I）求的值；

（II）在角A、B、C的对边分别是求的值。

正确答案

解：（I）

（II）

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

18．某商场准备在五一劳动节期间举行促销活动，根据市场调查，该商场决定从2种服装商品、3种家电商品、5种日用商品中，选出3种商品进行促销活动。

（I）试求选出的3种商品中至少有一种是日用商品的概率；

（II）商场对选出的A商品采用的促销方案是有奖销售，即在该商品现价的基础上将价格提高120元，同时允许顾客有3 次抽奖的机会，若中奖，则每次中奖都可获得60元奖金，假设顾客每次抽奖时获奖与否是等可能的。试求某位顾客所中奖金数不低于商场提价数的概率。

正确答案

解：（I）从2种服装商品，3种家电商品，5种日用商品中，选出3种商品，一共有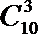种不同的选法。选出的3种商品中，没有日用商品的选法有种，所以选出的3种商品中至少有一种日用商品的概率为

（II）要使所中奖金数不低于商场提价数，则该顾客应中奖两次或三次，分别得奖金120元和180元。

顾客每次抽奖时获奖与否是等可能的，其概率都是

所以中奖两次的概率是：

中奖三次的概率是

故中奖两次或三次的概率：

即所中奖金数不低于商场提价数的概率等于

说明：其他解法请酌情给分。

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：简答题

分值: 12分

21．已知函数轴对称。

（I）求实数的值；

（II）求函数的单调区间；

（III）若直线的图象有3个不同的交点，求实数n的取值范围。

正确答案

解：（I）由

则，

由于函数轴对称

所以

（II）由（I）得

所以

解得；

令

所以函数单调递减。

（III）由（II）知，函数处有极大值，在处有极小值，

所以使直线的图象有3个不同交点，则须有

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

19．如图，在三棱锥P—ABC中，PA=2，AB=AC=4，点D、E、F分别为BC、AB、AC的中点。

（I）求证：平面PAD；

（II）求点A到平面PEF的距离；

（III）求二面角E—PF—A的正切值。

正确答案

: 解法一：

（I），

AD为PD在平面ABC内的射影。

又点E、F分别为AB、AC的中点，

在中，由于AB=AC，故

，平面PAD

（II）设EF与AD相交于点G，连接PG。

平面PAD，dm PAD,交线为PG，

过A做AO平面PEF，则O在PG上，

所以线段AO的长为点A到平面PEF的距离

在

即点A到平面PEF的距离为

说明：该问还可以用等体积转化法求解，请根据解答给分。

（III）

平面PAC。

过A做，垂足为H，连接EH。

则

所以为二面角E—PF—A的一个平面角。

在

即二面角E—PF—A的正切值为

解法二：

AB、AC、AP两两垂直，建立如图所示空间直角坐标系，

则A（0，0，0），E（2，0，0），D（2，2，0），F（0，2，0），P（0，0，2）

（I）

且

平面PAD

（II）为平面PEF的一个法向量，

则

令

故点A到平面PEF的距离为：

所以点A到平面PEF的距离为

（III）依题意为平面PAF的一个法向量，

设二面角E—PF—A的大小为（由图知为锐角）

则，

所以

即二面角E—PF—A的正切值为

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面垂直的判定与性质线面角和二面角的求法

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷