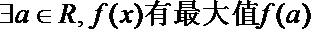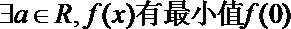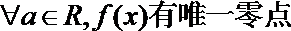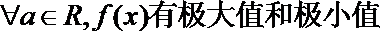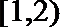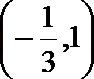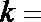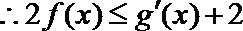- 真题试卷
- 模拟试卷
- 预测试卷
4.已知过点(1,2)的二次函数
①
②
③
④
其中正确论断是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.如图,程序框图的输出值
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知O.A.B是平面上的三点,向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数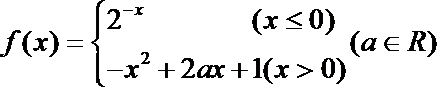
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列说法中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数f(x)的部分图象如图所示,则f(x)的解析式可能为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.直线l过点(

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若“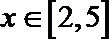
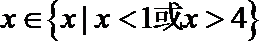
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设A和B是抛物线上的两个动点,且在A和B处的抛物线切线相互垂直, 已知由










则
正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
12.设集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.甲、乙两位同学各买了一件礼物送给丙、丁两人中的一人,则甲、乙两人将礼物送给了同一人的概率为__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,数学成绩如下表所示:
(I)为了了解同学们前段复习的得失,以便制定下阶段的复习计划,学校将采用分层抽样的方法抽取100名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,求他被抽中的概率;
(II)已知本次数学成绩的优秀线为110分,试根据所提供数据估计该中学达到优秀线的人数;
(III)作出频率分布直方图,并估计该学校本次考试的数学平均分.(同一组中的数据用该组区间的中点值作代表)
正确答案
解:(I)分层抽样中,每个个体被抽到的概率均为
故甲同学被抽到的概率
(II)由题意
故估计该中学达到优秀线的人数
(III)频率分布直方图.
该学校本次考试数学平均分

估计该学校本次考试的数学平均分为90分.
解析
解析已在路上飞奔,马上就到!
知识点
18.某建筑公司用8000万元购得一块空地,计划在该地块上建造一栋至少12层.每层4000平方米的楼房。经初步估计得知,如果将楼房建为x(x
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
正确答案
解:设楼房每平方米的平均综合费为

法一:
当且仅当
因此,当

为了使楼房每平方米的平均综合费最少,该楼房应建为20层,每平方米的平均综合费最小值为5000元
法二:
解析
解析已在路上飞奔,马上就到!
知识点
19.设数列
(I)求数列
(II)是否存在正整数n使得

正确答案
解:(I)




(II)

解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量
(I)求函数
(II)求函数
正确答案
解: (I)
(II)∵
令

∴对称点为
由
∴对称轴方程为
∵

∴
∴

解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆





(I)求椭圆的方程;
(II)证明

正确答案
解:(I)由题意,
解三角形得

从而


(II)设交点
联立

又直线

则有
从而



解析
解析已在路上飞奔,马上就到!
知识点
21.已知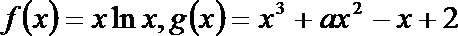
(I)如果函数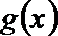
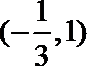
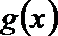
(II)在(Ⅰ)的条件下,求函数y=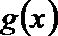
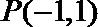
(III)若不等式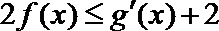
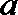
正确答案
解: (I)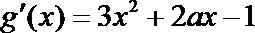
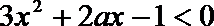
即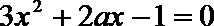
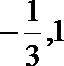
将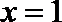
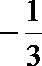
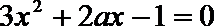
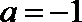
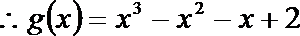
(II)由(Ⅰ)知: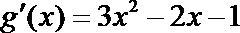
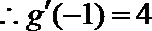
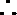
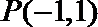
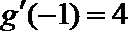
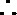
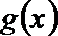
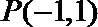
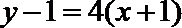
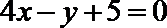
(III)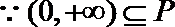
即: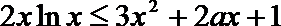
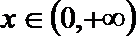
可得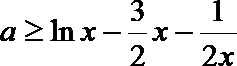
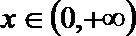
设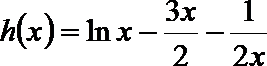
令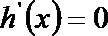
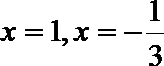
当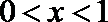
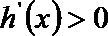
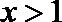
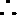
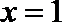
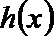
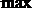
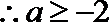
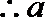
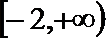
解析
解析已在路上飞奔,马上就到!