- 真题试卷
- 模拟试卷
- 预测试卷
3.下列说法正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知偶函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知向量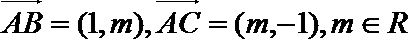
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数
①定义域为R;
②

③当
则方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. .若曲线y=

①y=cosx
②
③
④
⑤
有“好点”的曲线个数是____________。
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
13.已知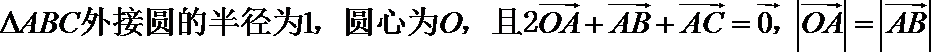
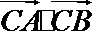
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
15. 以下命题:
①若


② 


③若△


④若非零向量



⑤已知△ABC中,

其中所有真命题的序号是____________。
正确答案
①②④⑤
解析
解析已在路上飞奔,马上就到!
知识点
16. 设命题p:实数x满足


(1)若


(2)若


正确答案
解:(1)当a=1时,1<x<3,即p为真时实数x的取值范围是1<x<3
由

若
(2) 若

设使命题p为真的x集合为A={x|a<x<3a},
设使命题q为真的x集合为
则B为A的真子集,
解析
解析已在路上飞奔,马上就到!
知识点
17. 



(1)判断
(2)设向量


正确答案
解:(1)由题

由正弦定理

又



即

(2)由于

且

联立①②解得

解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数
(1)求
(2)若将


正确答案
解:(1)
=
所以
(2)∵将



∴
∵
∴当
当
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数



(1)求
(2)若函数

正确答案
解:(1)把A(1,2),B(-1,1)代入
解得 a=2,b=3
f(x)=log2(x+3)
(2)
所以g(x) 的值域是
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列








(1)求数列



(2)若对任意的


(3)是否存在正整数


正确答案
(2)①当

即需不等式




②当

即需不等式








综合①、②可得

(3)
若

即
由

即

又



因此,当且仅当



[另解] 因为



解析
解析已在路上飞奔,马上就到!
知识点
21.已知

(1)若


(2)求
(3)设



正确答案
解: (1) 


经检验, 
(2) 
1) 当


2)当

① 若




②若



综上所述,当


当



(3)当


易知

∵
∴由题设知

故:

解析
解析已在路上飞奔,马上就到!