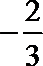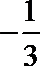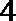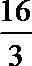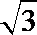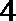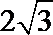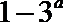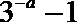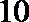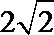- 真题试卷
- 模拟试卷
- 预测试卷
7.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知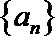
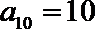


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 某几何体三视图如下,图中三个等腰三角形的直角边长都是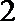
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若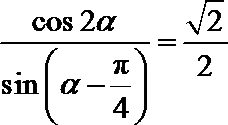
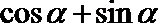
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 三棱锥




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.双曲线
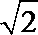
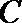
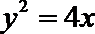
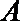
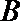
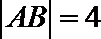
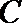
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 定义在R上的奇函数

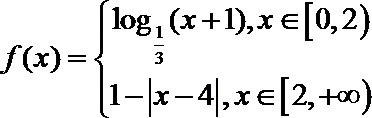

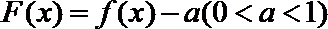
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知平面


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.执行如图程序框图其输出结果是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 在等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知变量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 向量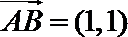



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)求函数

(2)将函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在三棱柱










(1)证明:
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.一个袋子中装有大小形状完全相同的

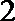

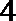
(1)从袋子中随机取出两个小球,求取出的小球编号之和大于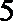
(2)先从袋子中取出一个小球,该球编号记为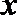

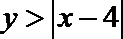
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆







(1)求椭圆
(2)已知点






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数

(1)若


(2)设函数


















正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请在第22、23、24三题中任选一题作答.
22.选修4-1:几何证明选讲
如图,


















(1)求证:
(2)若

23.选修4-4:坐标系与参数方程
已知点




(1)求点

(2)求
24.选修4-5:不等式选讲
已知正实数


(1)求

(2)设函数




正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!