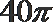- 真题试卷
- 模拟试卷
- 预测试卷
2．已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．设l，m，n是不同的直线，α，β是不同的平面，则下列命题正确的是（ ）
A若l∥m，m
B若l⊥m，l⊥n，m
C若α∥β，l
D若l
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知点P是双曲线
A4
B2
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．某程序框图如图所示，则该程序运行后输出的
A－1
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．某校高三文科两个班级共110位学生，其中75位学生参加了数学兴趣小组，80位学生参加了英语兴趣小组，那么既参加数学兴趣小组又参加英语兴趣小组的学生个数的最大值和最小值的差是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．已知函数f (x)＝
A0
B
C1
D10
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．在等比数列{an}中，若a2a4＝4，则a3＝（ ）
A
B2
C－2
D4
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．若实数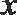
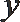
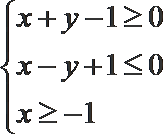
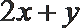
A
B
C1
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．如果函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．过圆
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
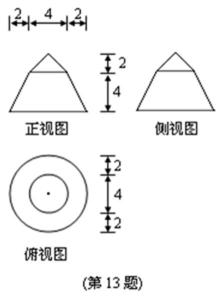
13．若某几何体的三视图(单位：cm)如图所示，则此几何体的体积是（ ）cm3．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．将函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．如图所示，在三棱柱ABC－A1B1C1中，AA1
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．据凤凰网关于个税起征点的最新调查，3000元支持率是7%，5000元的支持率是56%，8000元的支持率是24%，8000元以上的支持率是13%. 若按照分层抽样，从投票的网友中抽取200人参加分析讨论，则应在5000元的支持者中抽取________人．
正确答案
112
解析
解析已在路上飞奔，马上就到！
知识点
14．已知单位向量α，β，满足|α＋3β|＝|2α－β|，则α与β的夹角为 ______．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．点
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21．已知函数
（I）求f (x)的极值；
（II）已知
正确答案
(Ⅰ) 
所以，f (x)的极大值为f (0)＝0， f (x)的极小值为f (2)＝
( II ) 由上题可知，
由题意可知，
解析
解析已在路上飞奔，马上就到！
知识点
19．设首项为
(Ⅰ) 求
( II ) 若各项为正数的数列{
正确答案
（I）
求得
（I I）
即
两式相减，得
又
而
解析
解析已在路上飞奔，马上就到！
知识点
20．如图，在四棱锥
（Ⅰ）求证：
（II）求直线
正确答案
（I）
连接BD，交AC于O,连接EO
又
又
（I I）(定义法)过E作SC的垂线，垂足为F，连接FA
(另法：取SC中点为F，连接EF，上面的作图方法容易理
解，但是另法的作图方法容易证明，二者的证明略有不同)
又
EF＝
解析
解析已在路上飞奔，马上就到！
知识点
22．已知P是抛物线C：y2＝4x上的一个动点，Q(2, 2)是抛物线C所在平面上的一个定点，过抛物线C焦点F的直线
(Ⅰ)求|QP|+|PF|的最小值;
( II )分别过A,B两点作抛物线C的准线的垂线，垂足分别是D，E，求
正确答案
(Ⅰ)
过P点作抛物线C的准线的垂线，垂足为G，
则根据抛物线的定义，|PG|=|PF|，则|QP|+|PF|＝|QP|+|PG|，
三点Q，P，G共线时，|QP|+|PG|最短，
则|QP|+|PF|＝3
（II）设A（
则
设
故当
解析
解析已在路上飞奔，马上就到！
知识点
18． 在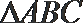
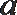
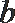
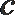
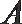
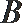
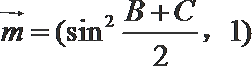
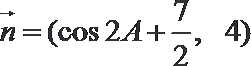
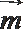
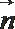
(Ⅰ) 求角
( II ) 当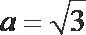
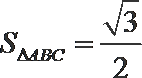
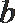
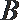
正确答案
解析
解析已在路上飞奔，马上就到！