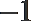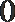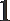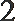- 真题试卷
- 模拟试卷
- 预测试卷
1.若复数


正确答案
解析
解析已在路上飞奔,马上就到!
3.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.公比不为






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.某班有24名男生和26名女生,数据


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若曲线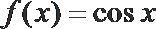
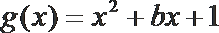
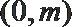
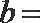
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.如图,若一个空间几何体的三视图中,正视图和侧视图都是直角三角形,其直角边长均为1,则该几何体的体积为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.变量









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知a是实数,则函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在平面直角坐标系








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.变量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知向量






正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
14.已知双曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知两个正四棱锥有公共底面,且底面边长为4,两棱锥的所有顶点都在同一个球面上.若这两个正四棱锥的体积之比为
正确答案
36π
解析
解析已在路上飞奔,马上就到!
知识点
17. 在△ABC中,角






(Ⅰ) 求证:


(Ⅱ) 若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在四棱锥







(Ⅰ )求证:
(Ⅱ )求三棱锥
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
由于工作疏忽,统计表被墨水污染,

(Ⅰ ) 若把频率看作概率,求

(Ⅱ ) 把日最高气温高于32℃称为本地区的“高温天气”,根据已知条件完成下面
附:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆





(Ⅰ )求椭圆
(Ⅱ )若







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设


(Ⅰ)讨论函数
(Ⅱ)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题:请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分。
22.选修4—1:几何证明选讲
如图,已知






(Ⅰ)求证:
(Ⅱ)求证:
23.选修4—4;坐标系与参数方程
已知曲线








(Ⅰ)求曲线
(Ⅱ)若点


24.选修
已知函数
(Ⅰ)当


(Ⅱ)若


正确答案
22.

23.

24.
解析
解析已在路上飞奔,马上就到!