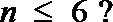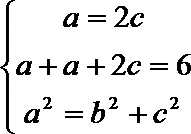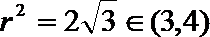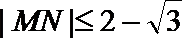- 真题试卷
- 模拟试卷
- 预测试卷
2.已知某个几何体的三视图如下图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知正项数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知正实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若复数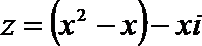
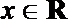

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知向量






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知点






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知角


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 某校高中部有三个年级,其中高三有学生



正确答案
3700
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,若程序框图输出的S是126,则判断框①中应为 ___________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知不等式组




正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
14.曲线









正确答案

解析
解析已在路上飞奔,马上就到!
知识点
12.







正确答案

解析
解析已在路上飞奔,马上就到!
知识点
16. 如图,在四棱锥







(Ⅰ)

(Ⅱ)平面

(Ⅲ)求四棱锥
正确答案
(3)略
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆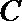
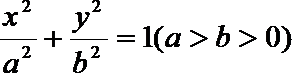
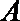
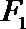
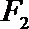
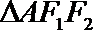
(Ⅰ)求椭圆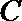
(Ⅱ)已知圆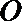
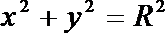
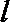

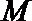
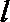
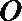
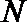
正确答案
(Ⅰ)解:由题设得
解得: 
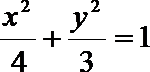
(Ⅱ)直线
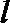

由直线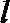
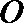
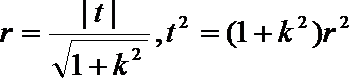
由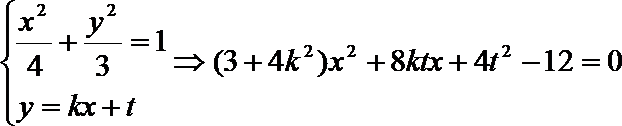
因为直线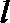
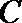
所以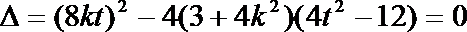
得
所以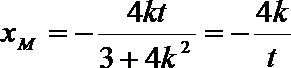
由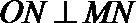
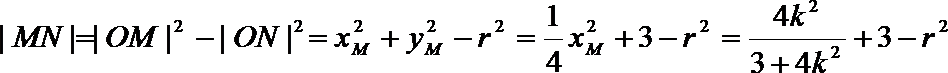
由①②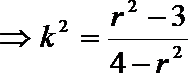
将④代入③得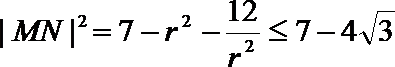
当且仅当
所以
解析
解析已在路上飞奔,马上就到!
知识点
20.将





(Ⅰ)当

(Ⅱ)当

正确答案
(Ⅰ)













(Ⅱ)
上式转化为
在上述





所以


若使
所以

解析
解析已在路上飞奔,马上就到!
知识点
17.从含有两件正品和一件次品的3件产品中,每次任取1件
(1)每次取出后不放回,连续取两次,求取出的产品中恰有一件次品的概率;
(2)每次取出后放回,连续取两次,求取出的产品中恰有一件次品的概率。
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数


(I)若曲线



(II)若函数
正确答案


(I)因为曲线


所以
(II)当

这时
当




对于

当

这时

解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
(Ⅰ)求函数
(Ⅱ)记



正确答案
(Ⅰ)
所以函数

(Ⅱ)由

又因为
所以

因为
所以由正弦定理
故
当
当
故
解析
解析已在路上飞奔,马上就到!