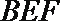- 真题试卷
- 模拟试卷
- 预测试卷
4.在各项均为正数的等比数列{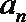
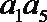
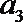
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若幂函数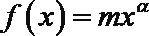
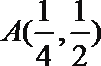
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设函数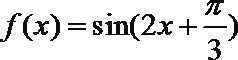
①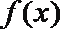
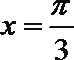
②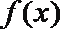
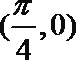
③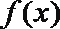
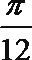
④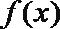
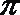
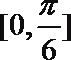
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 某几何体的三视图如图所示,且正视图、侧视图都是矩形,则该几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知为虚数单位,复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.称




①
②
③对任意的
则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.由直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 下列函数中,在其定义域内既是奇函数又是增函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.书架上有语文、数学、英语书若干本,它们的数量比依次是2:4:5,现用分层抽样的方法从书架上抽取一个样本,若抽出的语文书为10本,则应抽出的英语书______本.
正确答案
25
解析
解析已在路上飞奔,马上就到!
知识点
11.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.圆心在


正确答案

解析
解析已在路上飞奔,马上就到!
知识点
选做题(14、15题,只能从中选做一题)
14.(坐标系与参数方程选做题)
在极坐标系中,直线
15.(几何证明选讲选做题)
如图,






正确答案
14.
15.
解析
解析已在路上飞奔,马上就到!
知识点
16.在





求:
(I)
(II)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
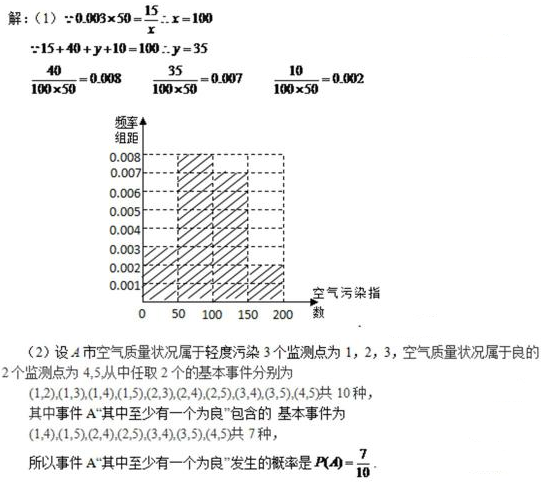
17.空气污染,又称为
(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知抛物线

(Ⅰ)求抛物线C的方程;
(Ⅱ)设过点M(0,2)的直线与抛物线C交于A,B两点,且A点的横坐标为
(ⅰ)记△AOB的面积为

(ⅱ)探究是否存在不同的点A,使对应不同的△AOB的面积相等?若存在,求点A点的坐标;若不存在,请说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(I)若

(II)若






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
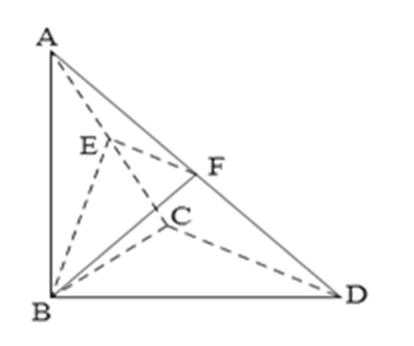
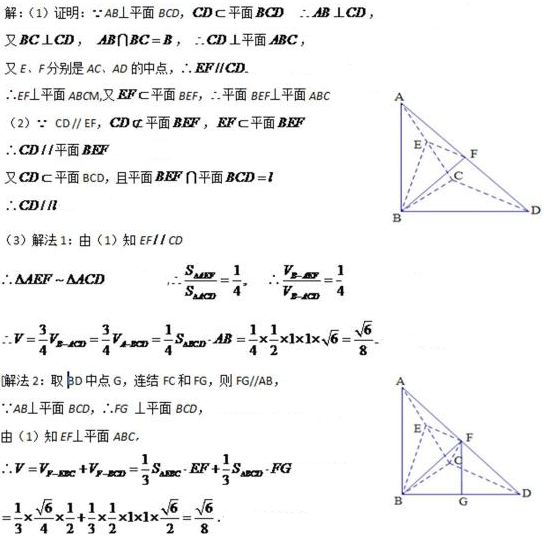
18.如图,已知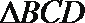
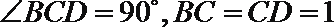
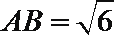


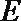
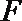
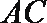
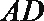
(1)求证:平面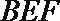
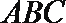
(2)设平面
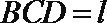
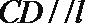
(3)求四棱锥B-CDFE的体积V.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设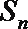
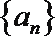
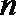
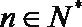
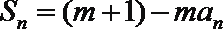
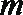
(1)求证:数列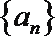
(2)数列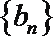
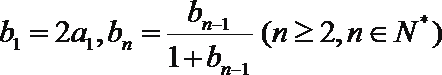
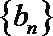
(3)在满足(2)的条件下,求数列
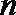
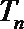
正确答案
解析
解析已在路上飞奔,马上就到!