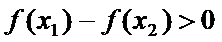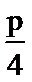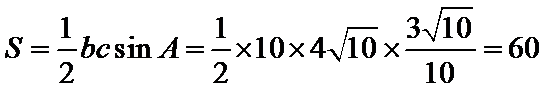- 真题试卷
- 模拟试卷
- 预测试卷
1. 若集合


正确答案
解析
解出集合B为
考查方向
解题思路
先解出集合B,然后用数轴将2个集合表示出来,找出交集。
易错点
本题易在解集合B的时候将区间写错 。
知识点
2. 已知i是虚数单位,复数
正确答案
解析


考查方向
解题思路
先解出复数Z,利用共轭复数的概念找出正确选项。
易错点
本题易在复数的分母有理化过程中不知道怎样化简,还有对共轭复数的概念不熟悉。
知识点
3. 已知向量



正确答案
解析
两个向量垂直
考查方向
解题思路
直接由垂直数量积为0构造关于m的一个方程解出即可。
易错点
本题垂直的时候不知道数量积为零。
知识点
5. 已知倾斜角为的直线


正确答案
解析
已知直线的斜率为


考查方向
解题思路
由垂直知所求直线的斜率,由斜率可知直线的倾斜角,利用诱导公式即可解出。
易错点
本题垂直的时候不知道斜率满足市民关系,三角函数的诱导公式不会用。
知识点
7. 右面程序框图运行后,如果输出的函数值在区间[-2,
正确答案
解析
当x<0时,由



考查方向
解题思路
分2类分别解出x的范围即可。
易错点
本题不知道对x进行分类讨论来解答。
知识点
12. 已知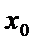
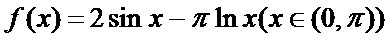
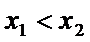
则①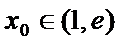
②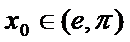
③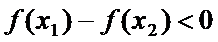
④
其中正确的命题是( )
正确答案
解析
由于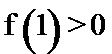
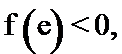
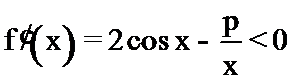
考查方向
解题思路
由零点存在定理找到第1个是正确的,然后利用导数找到函数的单调性从而找到第4个正确的。
易错点
本题不记得零点存在定理。
知识点
9. 设函数





正确答案
解析
根据在x=-2处取得极小值,则在x<-2时导数小于0,x>-2时导数大于0,等于-2时导数值等于0,所以在小于0的部分图像应该满足在x<-2在x轴上方,-2
考查方向
解题思路
根据在x=-2处取得极小值,则在x<-2时导数小于0,x>-2时导数大于0,等于-2时导数值等于0,然后导函数与x相乘之后可以根据正负找到正确的图像。
易错点
抽象函数没有具体解析式无法下手。
知识点
4. 在等比数列



正确答案
解析
两个向量垂直
考查方向
解题思路
直接由垂直数量积为0构造关于m的一个方程解出即可。
易错点
本题垂直的时候不知道数量积为零。
知识点
6. 已知




正确答案
解析
由已知可得T=

考查方向
解题思路
根据相邻两条对称轴之间的距离求出周期T,由周期求出


易错点
本题不会把相邻两条对称轴之间的距离转化为所学的内容。
知识点
8. 若



正确答案
解析
由题意可知经过点
考查方向
解题思路
由线性约束条件将可行域做出来,在分析在什么位置取到最大值,然后根据最大值为6得到一个关于k的方程,解方程即可得到答案。
易错点
本题在哪个位置取最值容易搞混淆。
知识点
11. 过点






正确答案
解析
由题意可以求出直线的方程为
考查方向
解题思路
过点
易错点
本题不会用数形结合来解答。
知识点
10. 一艘轮船从O点正东100海里处的A点处出发,沿直线向O点正北100海里处的B点处航行.若距离O点不超过r海里的区域内都会受到台风的影响,设r是区间[50,100]内的一个随机数,则该轮船在航行途中会遭受台风影响的概率约为( )
正确答案
解析
由题意知O到距离斜边的距离为

考查方向
解题思路
画出示意图,找到距离斜边的距离为
易错点
本题不能将题目转化为所学的知识去解答。
知识点
13. 函数
正确答案
(3,0)
解析
当x=3时,无论a的值是多少,其对数值都为0,所以答案为(3,0).
考查方向
解题思路
知道对数的真数为1即可。
易错点
本题不知道1的对数值恒为0。
知识点
14. 各项均为正数的等差数列


正确答案
72
解析
考查方向
解题思路
利用基本不等式得到第4项和第9项之和的最小值,然后利用等差数列的求和公式即可解出。
易错点
本题不知道联系基本不等式来解。
知识点
15. 如图所示,某几何体的三视图,则该几何体的体积为 。
正确答案
2
解析
还原出的直观图如下:

考查方向
解题思路
由三视图还原出原图的直观图是一个四凌锥。
易错点
本题不能由三视图将直观图想象出来。
知识点
16. 
正确答案
(3,3.5)
解析
由


考查方向
解题思路
对函数求导,根据导函数为3这个方程有2个大于0的根即可解出a的取值范围。
易错点
本题不知道转化为根的分布问题。
知识点
在
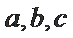
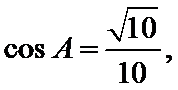
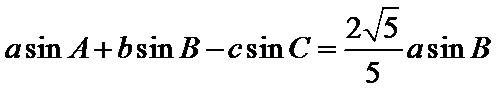
17. 求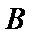
18. 设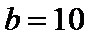
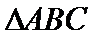
正确答案
解析
试题分析:本题属于解三角形的问题,(1)考查正余弦定理的综合应用,(2)考查正弦定理和三角形的面积公式。
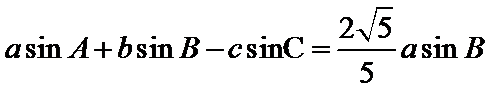
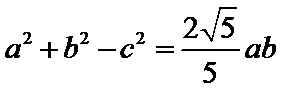
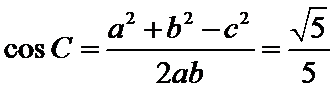
又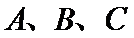
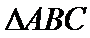
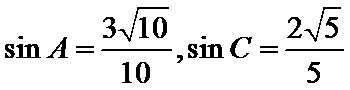
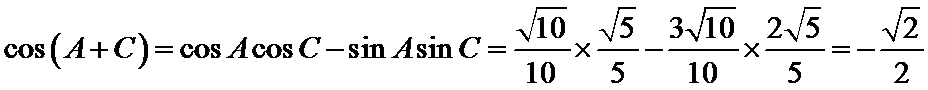
又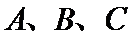
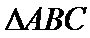
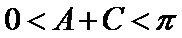
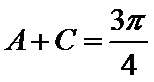
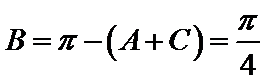
考查方向
解题思路
(1)根据正弦定理实现边角互化,然后用余弦定理求出角C的三角函数值,再进一步求出角B的三角函数值,最终确定角B的大小,
(2)由正弦定理求出c边,然后利用三角形的面积公式即可解出答案。
易错点
不知道用正弦定理实现边角互化。
正确答案
60
解析
试题分析:本题属于解三角形的问题,(1)考查正余弦定理的综合应用,(2)考查正弦定理和三角形的面积公式。
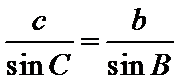
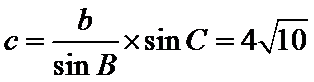
考查方向
解题思路
(1)根据正弦定理实现边角互化,然后用余弦定理求出角C的三角函数值,再进一步求出角B的三角函数值,最终确定角B的大小,
(2)由正弦定理求出c边,然后利用三角形的面积公式即可解出答案。
易错点
不知道用正弦定理实现边角互化。
函数

26.当a=1时,求函数
27.①若存在实数


②若有且只有唯一整数


正确答案



解析
试题分析:本题属于函数与导数的问题,(1)考查求函数的单调区间,(2)1.参数的取值范围,2.参数的取值范围。
当a=1时,

由于
当


当


所以


考查方向
解题思路
(1)利用导数与函数的单调性的关系来求,
(2)1.构造函数求解,
2.利用导数求解。
易错点
分类讨论的思想讨论不完全。
正确答案
1.a的取值范围为
2.a的取值范围为
解析
试题分析:本题属于函数与导数的问题,(1)考查求函数的单调区间,(2)1.参数的取值范围,2.参数的取值范围。
①由

当
当



记


∴ 




∴ 当



综上所述,所有a的取值范围为
②由①知



又



∴


当



又



∴

综上所述,所有a的取值范围为
考查方向
解题思路
(1)利用导数与函数的单调性的关系来求,
(2)1.构造函数求解,2.利用导数求解。
易错点
分类讨论的思想讨论不完全。
据统计,2015年“双11”天猫总成交金额突破






女性消费情况:
男性消费情况:
19.计算


20.若消费金额不低于



附:
(

正确答案
解析
试题分析:本题属于概率和独立性检验的问题,(1)考查古典概型和分层抽样,(2)独立性检验的思想。解:依题意,女性应抽取

抽出的










设“选出的两名网购者恰好是一男一女”为事件
事件


考查方向
解题思路
(1)根据分层抽样求出男女各抽的人数,然后用穷举法列举出基本事件的总数,找到要求的基本事件的个数,用古典概型公式可以算出其概率,
(2)利用独立性检验的方法解出。
易错点
不知道应用古典概型公式来计算。
正确答案
有关.
解析
试题分析:本题属于概率和独立性检验的问题,(1)考查古典概型和分层抽样,(2)独立性检验的思想。

则
答:我们有99%的把握认为“是否为‘网购达人’”与性别有关
考查方向
解题思路
(1)根据分层抽样求出男女各抽的人数,然后用穷举法列举出基本事件的总数,找到要求的基本事件的个数,用古典概型公式可以算出其概率,
(2)利用独立性检验的方法解出。
易错点
不知道应用古典概型公式来计算。
如图,在四棱锥






21.求证:

22.若




23.在(Ⅱ)的条件下,线段



正确答案
见解析
解析
试题分析:本题属于立体几何的问题,(1)线线平行的证明,(2)线面垂直的证明,(3)线面垂直是否存在的问题。
证明:因为底面
所以

又因为



所以

又因为


所以
考查方向
解题思路
(1)由线面平行最后得到线线平行的证明,
(2)利用线面垂直的判定定理,
(3)利用反证法求解。
易错点
不知道应用判定定理及性质定理去解答。
正确答案
见解析
解析
试题分析:本题属于立体几何的问题,(1)线线平行的证明,(2)线面垂直的证明,(3)线面垂直是否存在的问题。
在正方形

又因为平面

且平面

所以

又


由(Ⅰ)可知

又因为



由点



在△


又因为


考查方向
解题思路
(1)由线面平行最后得到线线平行的证明,
(4)利用线面垂直的判定定理,
(5)利用反证法求解。
易错点
不知道应用判定定理及性质定理去解答。
正确答案
见解析
解析
试题分析:本题属于立体几何的问题,(1)线线平行的证明,(2)线面垂直的证明,(3)线面垂直是否存在的问题。
不存在.假设线段


取AB中点N,连接NE,易知



线段


考查方向
解题思路
(1)由线面平行最后得到线线平行的证明,
(6)利用线面垂直的判定定理,
(7)利用反证法求解。
易错点
不知道应用判定定理及性质定理去解答。
如图椭圆



24.求椭圆
25.直线




(i)当

(ii)是否存在直线


正确答案
解析
试题分析:本题属于圆锥曲线的问题,(1)考查求椭圆的标准方程,(2)1.弦长公式,2.利用反正法最后推出矛盾。
考查方向
解题思路
(1)由已知条件很容易求出椭圆的方程,
(2)1.利用弦长公式即可解出,
2,利用反证法思想求解。
易错点
第2问不知道用设而不求的方法来解答且相对计算量点大。
正确答案
1.
2.不存在.
解析
试题分析:本题属于圆锥曲线的问题,(1)考查求椭圆的标准方程,(2)1.弦长公式,2.利用反正法最后推出矛盾。
(i)设点


设直线


化简得到
因为

所以

代入得到



(ii)圆心到直线


因为
代入得到
显然


考查方向
本题考查了椭圆的方程及直线和椭圆的位置关系。
解题思路
(1)由已知条件很容易求出椭圆的方程,
(2)1.利用弦长公式即可解出,2,利用反证法思想求解。
易错点
第2问不知道用设而不求的方法来解答且相对计算量点大。
如图,










28.求线段
29.求证:
正确答案
3
解析
试题分析:本题属于几何证明选讲的问题,(1)考查切割线定理,(2)相似三角形的判定。
因为

所以, 


所以
又

根据切割线定理得: 
即
考查方向
解题思路
(1)根据切割线定理可以解出,
(2)利用三角形相似对应边成比例。
易错点
不知道切割线定理使用。
正确答案
见详解.
解析
试题分析:本题属于几何证明选讲的问题,(1)考查切割线定理,(2)相似三角形的判定。
过


则

又由题意知

因此
考查方向
解题思路
(1)根据切割线定理可以解出,
(2)利用三角形相似对应边成比例。
易错点
不知道切割线定理使用。