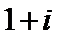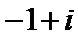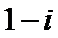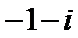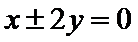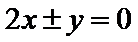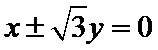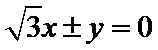- 真题试卷
- 模拟试卷
- 预测试卷
3.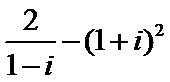
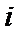
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知等差数列{




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下列函数中,在定义域内不是增函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若双曲线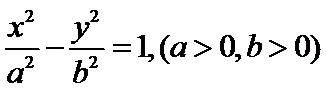
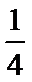
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设全集


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知某几何体的侧视图与其正视图相同,相关的尺寸如下图所示,则这个几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数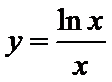
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.执行如图的程序框图,输出的S和n的值分别是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.以下说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在三棱锥P-ABC中,PA=PB=PC=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设数列












正确答案
2002
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆



(Ⅰ)求椭圆
(Ⅱ)过点










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(Ⅰ)求b的值;
(Ⅱ)当



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22.23.24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.如图,已知






(1)证明A,P,O,M四点共圆;
(2)求
23.选修4-4:坐标系与参数方程
过点



(1)写出直线
(2)求
(3)求
24.设对于任意实数x,不等式
(I)求m的取值范围;
(Ⅱ)当m取最大值时,解关于x的不等式:
22.如图,已知










(1)证明
(2)求
23.选修4-4:坐标系与参数方程
过点





(1)写出直线
(2)求
(3)求
24.设对于任意实数

(I)求m的取值范围;
(Ⅱ)当m取最大值时,解关于

正确答案
正确答案
正确答案
17. 已知函数
(Ⅰ)若


(II)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. C如图,矩形














(Ⅰ)求证:

(Ⅱ)若

(Ⅲ)求四面体
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),
(Ⅰ)下表是年龄的频数分布表,求正整数

(Ⅱ)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(Ⅲ)在(
正确答案
解析
解析已在路上飞奔,马上就到!