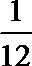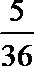- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合A={x|x>1},B={x|x≤5},则A∩B=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知直线ax-by-2=0与曲线y=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.一名同学先后投掷一枚骰子两
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm)。可得这个几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.给出计算



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知直线m、n与平面α、β,下列命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设函数f(x)=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列四个函数中,在区间(0,1)上是减函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.将函数f(x)=3sin(4x+

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知正方形ABCD的边长为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在三角形ABC中,若∠C=3∠B,则
正确答案
(1,3)
解析
解析已在路上飞奔,马上就到!
知识点
13.已知变量x、y满足条件
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
16.有下列命题:
①若



②将函数y=


③命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|≥2,则-2<x<2”;
④方程

⑤对于命题p:




其中假命题的序号是____________
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
20. 如下图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分,A(

(Ⅰ)求曲线C1和C2所在的椭圆和抛物线的方程;
(Ⅱ)过F2作一条与x轴不垂直的直线,与曲线C2
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请从22~24题中任选一道作答
22.选修4-1:几何选讲
如图所示,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.
(Ⅰ)求证:△DFE∽△EFA;
(Ⅱ)如果FG=1,求EF的长.
23.选修4-4:坐标系与参数方程.
在平面直角坐标系xOy中,曲线C1的参数方程为






(Ⅰ)分别说明C1、C2是什么曲线,并求出
(Ⅱ)设当α=


24.选修4-5:不等式选讲.
设函数
(Ⅰ)若a=-1,解不等式f(x)≥6;
(Ⅱ)如果
正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知{
(Ⅰ)求数列{
(Ⅱ)若{




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下:
(Ⅰ)求获得参赛资格的人数;
(Ⅱ)根据频率直方图,估算这500名学生测试的平均成绩.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数f(x)=lnx+
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.
(Ⅰ)求证:平面A1ED⊥平面A1AEF;
(Ⅱ)求三棱锥E-A1FD的体积.
正确答案
解析
解析已在路上飞奔,马上就到!