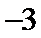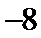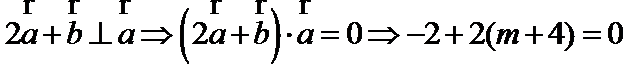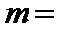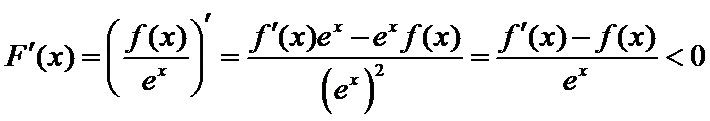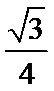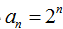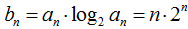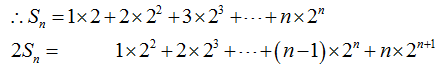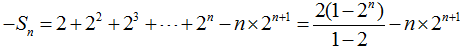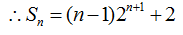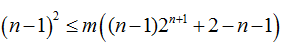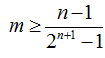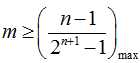- 真题试卷
- 模拟试卷
- 预测试卷
2.复数
正确答案
解析


考查方向
解题思路
先
易错点
本题易在计算上出现错误
知识点
4.已知向量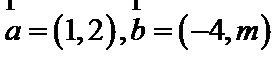
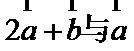
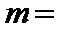
正确答案
解析
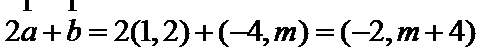
∴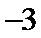
考查方向
解题思路
先求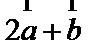
易错点
本题易在向量平行与垂直坐标运算混淆
知识点
5.已知x、y满足约束条件
正确答案
解析
做出如图可行域,
当目标函数经过C(4,0)时,截距最大,即

考查方向
解题思路
先根据约束条件画出可行域,再转化目标函数,把求目标函数最值问题转化成求截距的最值问题
易错点
本题易在不等式组表示表示平面区域表示错误
知识点
7.已知函数

正确答案
解析

∴
∴所以选项A为正确选项
考查方向
解题思路
先判断
易错点
本题易在分段函数的应用错误,判断不出变量范围
知识点
9.已知点



正确答案
解析
∵过







考查方向
解题思路
过


角形,

易错点
本题不会通过
知识点
3.下列函数中,既是奇函数,又是在区间
正确答案
解析
A. 












考查方向
解题思路
先求定义域,判断奇偶性,再利用性质判断单调性
易错点
本题易在函数指数函数、对数函数、幂函数混淆
知识点
6.下列说法错误的是( )
正确答案
解析
A.若










即

∴所以选项C为正确选项
考查方向
解题思路
逐个选项验证,分别判断它们的正误,其中ABD均正确,选项C的a值不能使两者同时成立,故可得答案.
易错点
本题易在充分必要条件的判定混淆使用
知识点
8.将函数

正确答案
解析
∵




考查方向
解题思路
先将

易错点
本题易在相位变换对变量
知识点
10.已知函数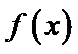
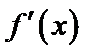
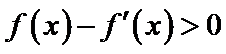
正确答案
解析
设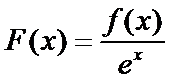
∴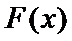
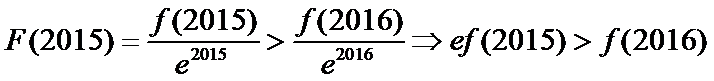
考查方向
解题思路
过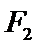
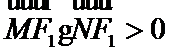
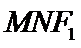
角形,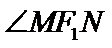
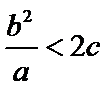
易错点
本题构造函数不正确得不到正确结论。
知识点
1.已知集合
正确答案
解析
∵
∴
∴
考查方向
解题思路
首先解绝对值不等式,得到集合A,然后求出交集即可
易错点
本题易在一元二次不等式解法上计算上出现错误
知识点
11.执行下图的程序框图,则输出的S=________.
正确答案
解析




考查方向
解题思路
分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S的值
易错点
本题易在程序框图读不懂,而且对积的导数容易求错;
知识点
13.如图茎叶图记录了甲、乙
正确答案
2
解析

∴
考查方向
解题思路
根据茎叶图,先求出x,再根据方差公式进行求解.
易错点
本题易在茎叶图上容易读错,要区分方差与标准差
知识点
14.已知M,N是圆


正确答案
解析
∵圆

圆
∴MN的方程为
∴
∴
考查方向
解题思路
先求出两圆的公共弦MN的方程,然后利用点B到直线MN的距离求出高BE,利用勾股定理求出MN即可
易错点
本题必须注意利用两圆相间得到公共弦方程
知识点
15.已知



正确答案
解析
如图所示
∵P,O,Q三点共线,则
∵
∴
∴
考查方向
解题思路
先利用向量的几何意义,利用三点共线,得出
易错点
本题不会利用三点共线转化
知识点
12.已知圆锥的侧面展开图是一个半径为3,圆心角为
正确答案
解析
∵圆锥侧面展开图是一个圆心角为120°半径为3的扇形∴圆锥的母线长为
形的弧长为

考查方向
解题思路
由于圆锥侧面展开图是一个圆心角为

易错点
本题必须注意圆锥侧面展开图是一个圆心角120°半径为3的扇形
知识点
17. 已知向量

(I)求函数
(II)在




正确答案
(1)


(2)
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求解:(I)
=
由
可得
所以函数的单调递增区间为[
(II)
由
考查方向
解题思路
本题考查三角函数与解三角形,解题步骤如下:
1、利用向量的数量积求出
2、利用余弦定理求出
易错点
第一问中的辅助角容易计算错误
知识点
19. 已知单调递增的等比数列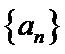
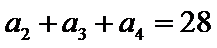
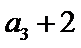
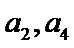
(I)求数列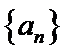
(II)设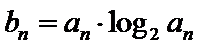
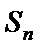
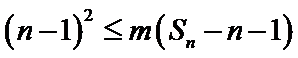
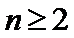
正确答案
(1)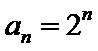
(2)
解析
试题分析:本题属于数列应用中的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求
(Ⅰ)设等比数列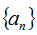
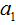
由题意可知: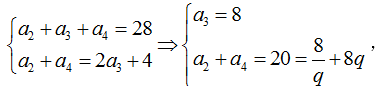
∴
所以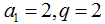
(Ⅱ)令
相减得
若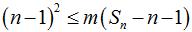
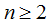
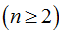
令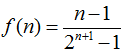
考查方向
解题思路
本题考查数列的性质,解题步骤如下:
1、利用基本量法求出通项;
2、利用错位相减法求和,恒成立问题转为最值问题
易错点
第一问中的辅助角容易计算错误
知识点
16. 根据我国发布的《环境空气质量指数(AQI)技术规定》:空气质量指数划分为0~50、51~100、101~150、151~200、201~300和大于300六级,对应于空气质量指数的六个级别,指数越大,级别越高,说明污染越,说明污染越严重,对人体健康的影响也越明显.专家建议:当空气质量指数小于150时,可以户外运动;空气质量指数151及以上,不适合进行旅游等户外活动.以下是济南市2015年12月中旬的空气质量指数情况:

(II)一外地游客在12月来济南旅游,想连续游玩两天,求适合旅游的概率.
正确答案
(1)
(2)
解析
试题分析:本题属于概率统计中的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求
考查方向
解题思路
本题考查概率统计,解题步骤如下:
1、直接列出基本事件总数
2、按照公式直接求解
易错点
第二问中的基本事件总数容易遗漏
知识点
18. 直三棱柱



(I)求证:MN//平面
(II)求证:

正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求
考查方向
解题思路
本题考查三角函数与解三角形,解题步骤如下:
1、利用中位线
2、转化证明
易错点
第一问中在平面

知识点
20. 设函数
(I)当

(II)当

正确答案
(1)f(x)极大值=f(1)=2,f(x)极小值=f=+ln 2;(2当a>2时,f(x)在和(1
当1<a<2时,f(x)在(0,1)和单调递减,在上单调递增.)
解析
试题分析:本题属于导数与函数的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求
(1)函数的定义域为(0,+∞).
当a=3时,f(x)=-x2+3x-ln x,f′(x)=
当<x<1时,f′(x)>0,f(x)单调递增;当0<x<及x>1时,f′(x)<0,f(x)单调递减.
所以f(x)极大值=f(1)=2,f(x)极小值=f=+ln 2
(2) f′(x)=(1-a)x+a-==,
当=1,即a=2时,f′(x)=-≤0,f(x)在定义域上是减函数;
当0<<1,即a>2时,令f′(x)<0,得0<x<或x>1;令f′(x)>0,得<x<1
当>1,即1<a<2时,由f′(x)>0,得1<x<;由f′(x)<0,得0<x<1或x>,
综上,当a=2时,f(x)在(0,+∞)上是减函数;
当a>2时,f(x)在和(1
当1<a<2时,f(x)在(0,1)和单调递减,在上单调递增.
考查方向
解题思路
本题考查导数的性质,解题步骤如下:
1、求导,然后解导数不等式,算极值。
2、求导,解不等式化,注意分类讨论
易错点
第一问中的导数的计算错误,、第二问中的易丢对a的分类讨论。
知识点
21. 平面直角坐标系




(I)求椭圆C的标
(II)设点A,B分别是椭圆的左、右顶点,若过点
(i)求证:
(ii)求
正确答案
(1)
(2)
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求
(1)

所以
所以椭圆的标准方程为
(II)(i)当AB的斜率为0时,显然
当AB的斜率不为0时,设

整理得





(ii)
当且仅当



方法二(i)由题知,直线AB的斜率存在,设直线AB的方程为:
设


则


(ii)
点




令

当且仅当




考查方向
解题思路
本题考查平面几何,解题步骤如下:1、利用椭圆的几何性质,结合离心率及隐含条件a2=b2+c2联立方程组求解a2,b2的值,则椭圆方程可求;2、利用


易错点
1、计算的准确性2利用基本不等式求出最值