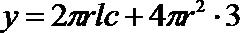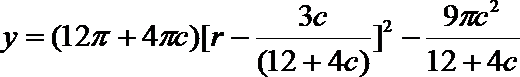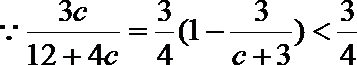- 真题试卷
- 模拟试卷
- 预测试卷
3.已知函数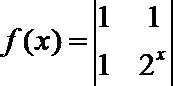
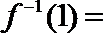
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
4.若复数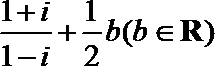
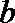
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图,水平放置的正三棱柱
正确答案
解析
解析已在路上飞奔,马上就到!
知识点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知平面上四点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.某班级有3名学生被复旦大学自主招生录取后,大学提供了3个专业由这3名学生选择,每名学生只能选择一个专业,假设每名学生选择每个专业都是等可能的,则这3个专业恰有一个专业没有学生选择的概率是_______.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在直角坐标平面上,有




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若对任意正实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 下列函数中,与函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 角


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 一无穷等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.下图揭示了一个由区间



















正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知复数



(1)若

(2)若


正确答案
(1)解法1、由题可知:



∴
解法2、
由题可知:

∵

解法3、
设
(2)解法1、
由(1)

∴
∵

∴
解法2、
由题意得:
则
则点

又
解法3、

即:


∴
则
解法4、根据坐标的几何意义求面积
解析
解析已在路上飞奔,马上就到!
知识点
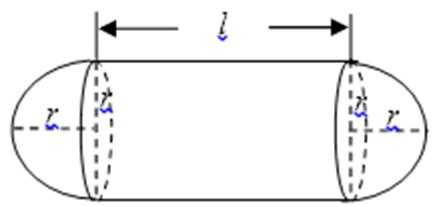
20.某加油站拟造如图所示的铁皮储油罐(不计厚度,长度单位:米),其中储油罐的中间为圆柱形,左右两端均为半球形,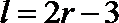
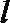
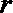

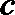

(1)写出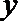

(2)求该储油罐的建造费用最小时的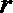
正确答案
(1)
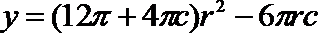
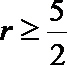
(2)
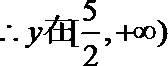
所以当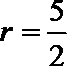
解析
解析已在路上飞奔,马上就到!
知识点
21.已知
(1)当



(2)试证函数

正确答案
(1)由

又

所以
(2) 

所以

解析
解析已在路上飞奔,马上就到!
知识点
22.已知椭圆







(1)求椭圆C的方程;
(2) 当

正确答案
(1)由题意得
则
所以椭圆

(2)

则
设


当且仅当
所以

解析
解析已在路上飞奔,马上就到!
知识点
23.如果数列






(1)若数列
(2)若数列

(3)若数列


正确答案
(1)当



因为

故
(2)当


所以数列
设公比为

即
所以
解得

所以
(3)存在常数
(或从必要条件入手
证明如下:因为
所以
由于
得
所以
即当
因为
所以
所以对任意
此时
解析
解析已在路上飞奔,马上就到!