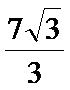- 真题试卷
- 模拟试卷
- 预测试卷
2.设


正确答案
解析

考查方向
解题思路
复数的除法,分母实数化
易错点
运算,概念
知识点
6.已知点(3,9)在函数


正确答案
解析







考查方向
解题思路
利用反函数的定义求解
易错点
反函数的定义
知识点
10.已知△ABC的三边长分别为3,5,7,则该三角形的外接圆半径等于____.
正确答案
解析
设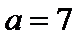
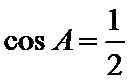
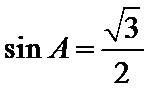
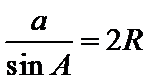
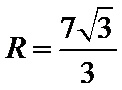
考查方向
解题思路
利用余弦定理得余弦值,利用基本关系求正弦值,利用正弦定理求半径.
易错点
正弦定理几何意义
知识点
1.设

正确答案
解析




考查方向
解题思路
利用绝对值不等式的解法
易错点
结果用集合或区间表示
知识点
3.已知平行直线



正确答案
解析
利用平行线间距离公式得:
考查方向
解题思路
平行线间距离公式;也可以转化为点到直线距离公式
易错点
用错公式
知识点
4.某次体检,5位同学的身高(单位:米)分别为1.72,1.78,1.80,1.69,1.76,则这组数据的中位数是______(米).
正确答案
解析
排序1.69,1.72, 1.76,1.78,1.80, 所以中位数是1.76.
考查方向
解题思路
排序,中间一个数就是中位数;如果中间是两个数,就取他们的平均值
易错点
概念
知识点
5.若函数

正确答案
解析


考查方向
解题思路
利用三角变换转化为一角一函数
易错点
一角一函数的转化方法
知识点
7.若


正确答案
解析
设





考查方向
解题思路
画图,利用目标函数的几何意义求解
易错点
平移法,最值的意义
知识点
8.方程

正确答案
解析





考查方向
解题思路
利用二倍角公式,恒等变形,转化为关于

易错点
换元思想解方程,求角
知识点
9.在
正确答案
解析
二项式系数和为256,所以





考查方向
解题思路
利用二项式系数和解出

易错点
二项式系数概念,计算
知识点
12.如图,已知点O(0,0),A(1.0),B(0,−1),P是曲线

正确答案
解析
因为A(1.0),B(0,−1),所以






考查方向
解题思路
向量坐标运算,三角变换,求最值
易错点
单位圆上点的坐标表示
知识点
14.无穷数列{an}由k个不同的数组成,Sn为{an}的前n项和.若对任意的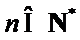
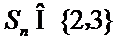
正确答案
解析
由于 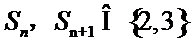
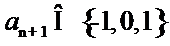
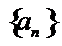
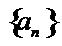
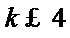
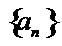
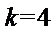
考查方向
解题思路
归纳,推理
易错点
推理的切入点
知识点
11.某食堂规定,每份午餐可以在四种水果中任选两种,则甲、乙两同学各自所选的两种水果相同的概率为______.
正确答案
解析
从4种水果中选择2种,共有6种选法,甲乙挑选同一种水果的方法占其中1种,依据古典概型知概率为
考查方向
解题思路
古典概型
易错点
事件的个数
知识点
13.设a>0,b>0. 若关于x,y的方程组

正确答案
解析








考查方向
解题思路
由方程组无解转化为直线平行,得
易错点
等号成立的条件
知识点
15.设
正确答案
解析
“a>1” 

考查方向
解题思路
充分条件,必要条件
易错点
定义
知识点
16.如图,在正方体ABCD−A1B1C1D1中,E、F分别为BC、BB1的中点,
则下列直线中与直线EF相交的是( )
正确答案
解析
直线B1C1和直线EF在同一平面内,又不平行,所以一定相交,其余选项都是异面直线.
考查方向
解题思路
空间直线的位置关系
易错点
空间想象
知识点
18.设f(x)、g(x)、h(x)是定义域为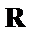
正确答案
解析
(1) 为假命题,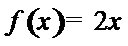
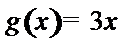

(2) 为真命题.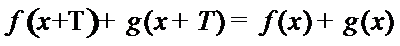
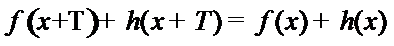
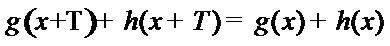
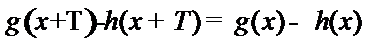
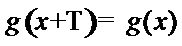
考查方向
解题思路
特殊函数举反例,方程思想解决f(x)、g(x)、h(x)均是以T为周期的函数
易错点
方程思想
知识点
17.设


正确答案
解析





考查方向
解题思路
三角函数值相等,考虑角的关系
易错点
讨论
知识点
题(本大题共有5题,满分74分)解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
本题共有2个小题,第1小题满分6分,第2小题满分6分.
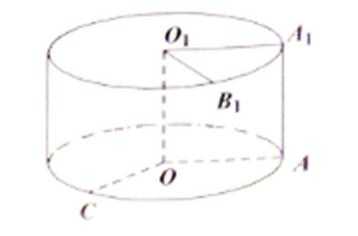
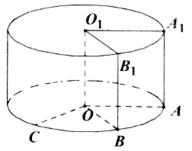
将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,
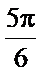
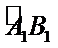
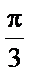
19.求圆柱的体积与侧面积;
20.求异面直线O1B1与OC所成的角的大小.
正确答案
圆柱的体积为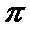
解析
由题意可知,圆柱的母线长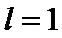
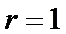
圆柱的体积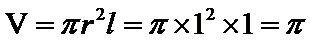
圆柱的侧面积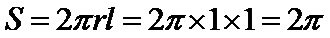
考查方向
解题思路
体积面积公式
易错点
用错公式
正确答案
异面直线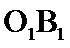
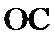
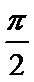
解析
设过点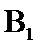
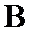
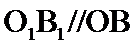
所以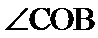
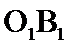
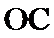
由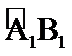
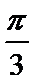
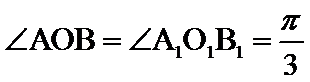
由
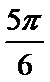
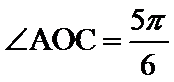
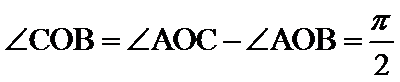
所以异面直线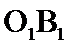
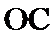
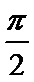
考查方向
解题思路
平移法解决异面直线夹角问题;
易错点
弧长公式
本题共有2个小题,第1小题满分6分,第2小题满分8分.
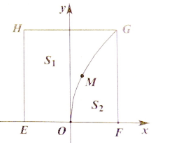
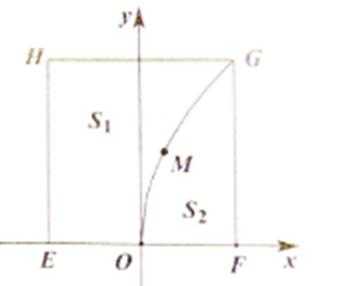
有一块正方形菜地EFGH,EH所在直线是一条小河,收获的蔬菜可送到F点或河边运走.于是,菜地分为两个区域S1和S2,其中S1中的蔬菜运到河边较近,S2中的蔬菜运到F点较近,而菜地内S1和S2的分界线C上的点到河边与到F点的距离相等.现建立平面直角坐标系,其中原点O为EF的中点,点F的坐标为(1,0),如图
21.求菜地内的分界线C的方程;
22.菜农从蔬菜运量估计出S1面积是S2面积的两倍,由此得到S1面积的“经验值”为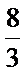
正确答案
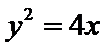
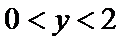
解析
因为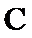
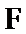
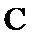
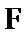
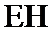
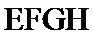
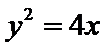
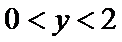
考查方向
解题思路
根据抛物线定义得到C的方程
易错点
题意的理解
正确答案
五边形面积更接近于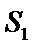
解析
解:
依题意,点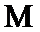
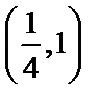
所求的矩形面积为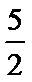
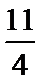
矩形面积与“经验值”之差的绝对值为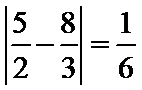
的绝对值为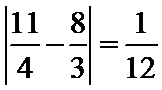
考查方向
解题思路
求出面积,根据题意比较和经验值的差距.
易错点
题意的理解
本题共有2个小题,第1小题满分6分,第2小题满分8分.
双曲线
23.若l的倾斜角为

24.设
正确答案
双曲线的渐近线方程为
解析
解:设
由题意,


因为

即

故双曲线的渐近线方程为
考查方向
解题思路
利用等边三角形的性质和双曲线中

易错点
弦长的运算
正确答案
斜率为
解析
解:
由已知,
设


由

因为


由


故
解得


考查方向
解题思路
联立方程组,根据弦长公式求出斜率.
易错点
弦长的运算
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
已知


28.当

29.若关于



30.设




正确答案
解析
由

解得
考查方向
解题思路
一般的解不等式
易错点
分类讨论,转化思想,
正确答案

解析

等价于

当

当


综上,

考查方向
解题思路
直接求方程的跟
易错点
分类讨论,转化思想,
正确答案


解析
当


所以

函数






因为



有最小值


故

考查方向
解题思路
根据单调性求最值.
易错点
分类讨论,转化思想,
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
对于无穷数列{















25.若





26.若




27.若{





正确答案


解析
因为


从而

考查方向
解题思路
用特殊值验证,得出不满足互补
易错点
理解题意
正确答案
180
解析
因为

数列


考查方向
解题思路
数列求和
易错点
计算
正确答案

解析
解:
设



由


若




若



综上,

考查方向
解题思路
设出等差数列的通项公式,推理论证.
易错点
公式的掌握和具体计算