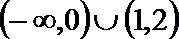- 真题试卷
- 模拟试卷
- 预测试卷
2.条件

正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
3.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.将函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.一人口袋里装有大小相同的



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若奇函数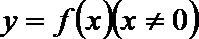
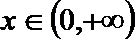
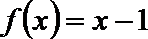
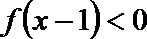
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知命题“已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.图中离散点是数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.直角坐标平面内,我们把横坐标.纵坐标都是整数的点称为整点。现有一系列顶点都为整点的等腰直角三角形







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.等比数列







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下:
根据表中的数据,将各行业按就业形势由差到好排列,其中排列正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.行驶中的汽车,在刹车时由于惯性的作用,要继续往前滑行一段距离才能停下,这段距离称为刹车距离。在某种路面上,某种型号汽车的刹车距离





(1)求
(2)要使刹车距离不超过12.6米,则行驶的最大速度应为多少?
正确答案
(1)
(2)
∴行驶的最大速度应为
解析
解析已在路上飞奔,马上就到!
知识点
17.已知关于

(1)设

(2)求
正确答案
(1)设实数解为

∴
(2)

∴
解析
解析已在路上飞奔,马上就到!
知识点
19.记函数



(1)求
(2)若


正确答案
(1)
(2)





解析
解析已在路上飞奔,马上就到!
知识点
20.已知


(1)设





(2)对于任意



正确答案
(1)





∴

(2)若



∴
∴


∴
解析
解析已在路上飞奔,马上就到!
知识点
21.设
(1)求

(2)讨论

(3)令





正确答案
(1)
(2)设
∴

∴



∴

(3)当
∵

∴
由

即
可知方程的两个根均大于
即
当


∴
综上,得 
解析
解析已在路上飞奔,马上就到!
知识点
22.已知数列



(1)求数列
(2)令





正确答案
(1)令

即
由

∵
∴
即数列


∴
(2)①
即
②∵
又∵

∴各项中数值最大为
∵对一切正整数

∴
解析
解析已在路上飞奔,马上就到!