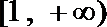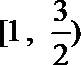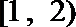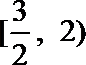- 真题试卷
- 模拟试卷
- 预测试卷
3.若函数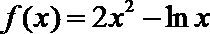
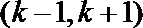
正确答案
解析
因为函数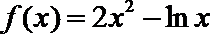
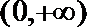
由
由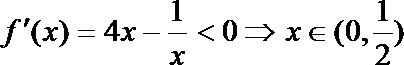
知函数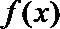
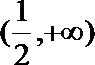
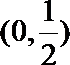
因此要使函数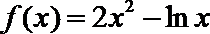
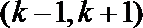
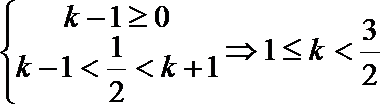
知识点
4.如果


正确答案
解析
首先当



其次当


必须且只需:


知识点
9.已知实数列

正确答案
解析
因为实数列




知识点
10.如图,正方形







正确答案
解析



知识点
1.已知全集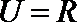
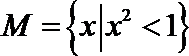
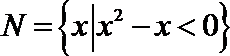
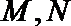
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.不等式
正确答案
解析
因为不等式
知识点
5.若实数



正确答案
解析
由φ(a,b)=0得





知识点
6.命题“所有能被2整除的整数都是偶数”的否定是( )
正确答案
解析
命题“所有能被2整除的数都是偶数”是一个全称命题,其否定一定是一个特称命题,故排除A,B;结合全称命题的否定方法,我们易得:命题“所有能被2整除的数都是偶数”的否定应为:“存在一个能被2整除的整数不是偶数”
知识点
7.一个简单几何体的主视图、侧视图如图所示,则其俯视图不可能为 :
①长、宽不相等的长方形;
②正方形;
③ 圆;
④ 椭圆.
其中正确的是( )
正确答案
解析
由题设条件知,正视图中的长与侧视图中的长不一致
对于①,俯视图是长方形是可能的,比如此几何体为一个长方体时,满足题意;
对于②,由于正视图中的长与宽,侧视图是正方形,几何体不是正方体,故俯视图不可能是正方形;
对于③,由于正视图中的长与侧视图中的长不一致,几何体不是圆柱,故俯视图不可能是圆形;
对于④,如果此几何体是一个三棱柱,满足正视图中的长与侧视图中的长不一致,故俯视图可能是三角形,也可以是直角三角形.
综上知②③是不可能的图形.
知识点
8.正项等比数列{




正确答案
解析
由题意知正项等比数列{an}的公比为q(q≠1且q>0)
由


即q2-q-1=0
解得

故答案为:
知识点
11.已知
正确答案
解析
首先作出不等式组


知识点
12.设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若




正确答案
解析
由已知,不妨设C(c,0),D(d,0),A(0,0),B(1,0),
由题意有(c,0)=λ(1,0),(d,0)=μ(1,0)
所以λ=c,μ=d,代入

若C是线段AB的中点,则c=
d不存在,故C不可能是线段AB的中点,A错误;
同理B错误;
若C,D同时在线段AB上,则

得c=d=1,此时C和D点重合,与条件矛盾,故C错误.
故选:D.
知识点
15.已知P,Q为抛物线

正确答案
-4
解析
因为点P,Q的横坐标分别为4,-2
代入抛物线方程得P,Q的纵坐标分别为8,2.
由x2=2y,则
过点P,Q的抛物线的切线的斜率分别为4,-2
所以过点P,Q的抛物线的切线方程分别为y=4x-8,y=-2x-2
联立方程组解得x=1,y=-4
故点A的纵坐标为-4.
故答案为:-4.
知识点
16.某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第








正确答案
(2,403)
解析
根据题意,




将上述k个式子相加得,
同理由



将上述k个式子相加得,
∴第2012棵树种植点的坐标为(2,403).
故答案为(2,403).
知识点
13.若对任意x>0,
正确答案
[
解析
因为x>0,所以



知识点
14.若函数
正确答案
2
解析
∵函数
令
故f(x)的最大值M等于g(x)的最大值m加上1,即 M=m+1.
f(x)的最小值N等于g(x)的最小值n加上1,即N=n+1.
再由于g(x)是奇函数,由奇函数的性质可得 m+n=0
故M+N=m+1+n+1=2
知识点
17.已知函数
(Ⅰ)证明:
(Ⅱ)求不等式:
正确答案
(Ⅰ)
当

(Ⅱ)由(1)可知, 当
当


当


综上,不等式

解析
解析已在路上飞奔,马上就到!
知识点
18.



(Ⅰ)求角
(Ⅱ)若




正确答案
(Ⅰ)在

而

(Ⅱ)由

同理
∴
∵

∴


解析
解析已在路上飞奔,马上就到!
知识点
20.对某校高三年级学生参加社区服务次数进行统计,随机抽取

(Ⅰ)求出表中

(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
正确答案
(Ⅰ)由分组

所以


所以
(Ⅱ)因为该校高三学生有240人,分组

所以估计在此区间内的人数为
(Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有
设在区间



则任选


而两人都在

解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列




(Ⅰ)求
(Ⅱ)求数列
正确答案
(Ⅰ)当





∴c=2.∵a2=4,即
∴

综上所述
(Ⅱ)
则
(1)

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数


(I)求函数
(II)若对于区间



(III)若过点


正确答案
(I)

即

(II)令


则对于区间[-2,2]上任意两个自变量的值

所以

(Ⅲ)设切点为




因为过点

所以方程
即函数
则


解析
解析已在路上飞奔,马上就到!
知识点
21.已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品

(1)写出年利润

(2)年产量为多少千件时,该企业生产此产品所获年利润最大?(注:年利润=年销售收入-年总成本)
正确答案
(1)当

当

(2)①当




当





②当

当且仅当


综合①、②知

所以为9千件时,该企业生产此产品获利最大.
解析
解析已在路上飞奔,马上就到!