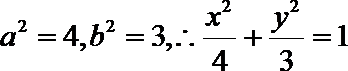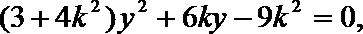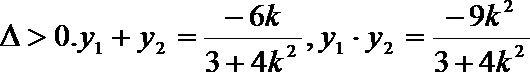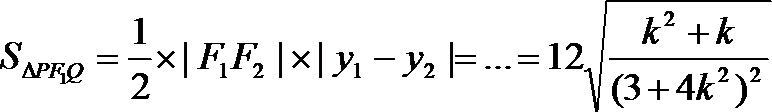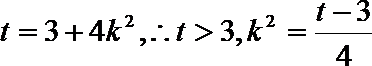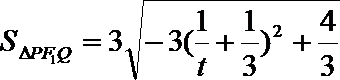- 真题试卷
- 模拟试卷
- 预测试卷
1.设i是虚数单位,则复数 的虚部是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.一个几何体按比例绘制的三视图如图所示(单位:m),该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知双曲线C1:

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知an=log(n+1)(n+2)(n∈N*).我们把使乘积a1·a2·a3·…·an为整数的数n叫做“优数”,则在区间(1,2004)内的所有优数的和为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 能够把圆



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知命题

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.以下四个命题:其中真命题为( )
①从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在回归直线方程
④对分类变量X与Y,它们的随机变量K2的观测值k来说,k越小,“X与Y有关系”的把握程度越大.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.程序框图如图所示:
如果上述程序运行的结果S=1320,那么判断框中应填入( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知菱形ABCD的边长为4,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知向量a,b,c满足


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在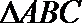
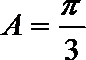
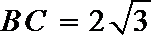
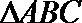
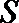
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如图是甲、乙两名篮球运动员2013年赛季每场比赛得分的茎叶图,则甲、乙两人比赛得分的中位数之和为___________.
正确答案
54
解析
解析已在路上飞奔,马上就到!
知识点
15.在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AC1、A1B1的中点.点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.函数

把函数


(1)若直线




(2)已知






正确答案
(1)由函数


又
由图像变换,得
由函数图像的对称性,有
(2)∵ 
∵ 

∴ 

∵ 

由正弦定理 

∵ 

解方程组①②,得
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)当


(2)当

(3)当



正确答案
(1)


(2)
(3)当

问题等价于

当

令

故

由于
所以存在

则

即
知








解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆C的左、右焦点分别为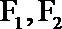

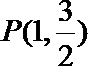
(1)求椭圆C的标准方程;
(2)若线段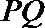
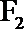
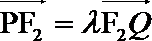
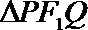
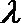
正确答案
(1)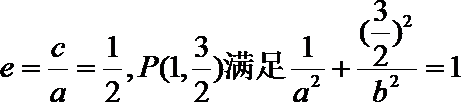
(2)显然直线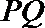
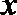
当直线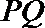
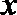
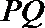
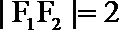
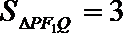
当直线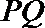
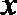
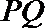
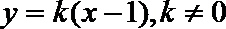
整理,得
令
所以
由上,得
所以当直线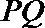
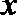
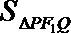
设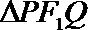
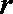
即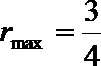
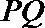
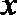
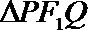
所以,
解析
解析已在路上飞奔,马上就到!
知识点
18.2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
附:
正确答案
(1)由题意可得列联表:
因为
所以能在犯错率不超过0.001的前提下,为该区学生常吃零食与患龋齿有关系。
(2)设其他工作人员为丙和丁,4人分组的所有情况如下表
分组的情况总有6中,工作人员甲负责收集数据且工作人员乙负责处理数据占两种,
所以工作人员甲负责收集数据且工作人员处理数据的概率是
解析
解析已在路上飞奔,马上就到!
知识点
请考生在22,23,24三题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-1:几何证明选讲
已知










(Ⅰ)求证:

(Ⅱ)求
选修4 - 4:坐标系与参数方程选讲
23.在直角坐标系中,曲线C的参数方程为

以原点为极点,x轴的正半轴为极轴建立极坐标系,点
为
(1)判断点
(2)设直线l与曲线C的两个交点为A、B,求
选修4 - 5:不等式选讲
24.已知函数
(1)解不等式
(2)若

正确答案
22.解:(Ⅰ)连结


因为




所以



(Ⅱ)由(Ⅰ)知
连结



所以

23.(1)直线






(2)直线


曲线C的直角坐标方程为
将直线
有
设两根为

24.(1)f(x)+f(x+4)=|x-1|+|x+3|=
当x<-3时,由-2x-2≥8,解得x≤-5;
当-3≤x≤1时,f(x)≤8不成立;
当x>1时,由2x+2≥8,解得x≥3. …4分
所以不等式f(x)≤4的解集为{x|x≤-5,或x≥3}.
(2)f(ab)>|a|f(),即|ab-1|>|a-b|.
因为|a|<1,|b|<1,
所以|ab-1|2-|a-b|2
=(a2b2-2ab+1)-(a2-2ab+b2)
=(a2-1)(b2-1)>0,
所以|ab-1|>|a-b|.故所证不等式成立.
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,正△ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求棱锥E-DFC的体积;
(3)在线段BC上是否存在一点P,使AP⊥DE?如果存在,求出
正确答案
(1)AB∥平面DEF,理由如下:
如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
又AB⊄平面DEF,EF⊂平面DEF.
∴AB∥平面DEF.
(2)∵AD⊥CD,BD⊥CD,将△ABC沿CD翻折成直二面角A-DC-B.
∴AD⊥BD
∴AD⊥平面BCD
取CD的中点M,这时EM∥AD
∴EM⊥平面BCD,EM=1,
(3)在线段BC上存在点P,使AP⊥DE
证明如下:在线段BC上取点P.使BP=BC/3, 过P作PQ⊥CD于Q,
∵AD⊥平面BCD
∴PQ⊥平面ACD
∴DQ=DC/3=2√3/3,
∴tan∠DAQ=DQ/AD═(2√3/3)/2=√3/3,
∴∠DAQ=30° 在等边△ADE中,∠DAQ=30°
∴AQ⊥DE
∵PQ⊥平面ACD
∴AP⊥DE.AQ∩AP=A
∴DE⊥平面APQ, ∴AP⊥DE.
此时BP=BC/3, ∴BP/BC=1/3.
解析
解析已在路上飞奔,马上就到!