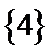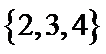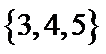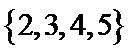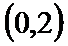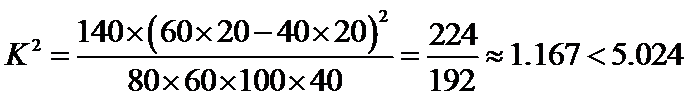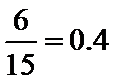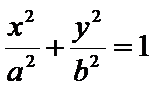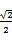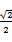- 真题试卷
- 模拟试卷
- 预测试卷
1. 已知全集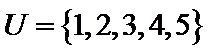
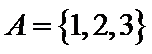
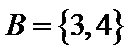
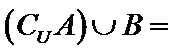
正确答案
解析
A在U中的补集={4,5},再求与B的并集
考查方向
解题思路
先求补集,再求并集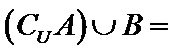
易错点
补集、并集掌握不熟
知识点
3. “


正确答案
解析
圆心坐标(a,3),半径R=2






考查方向
解题思路
由相切可知,圆心到直线的距离等于半径R,解出a=3,a=-5,与a=5对比
易错点
圆心到直线的距离易求错
知识点
4.已知数列



正确答案
解析
因为











考查方向
解题思路
首先整理关系是





易错点
容易在指数运算、对数运算出错
知识点
7. 右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的

正确答案
解析
按程序框图执行程序,a=4,b=10,a

a




考查方向
解题思路
直接按照程序框图执行程序即可。
易错点
不能正确的理解程序框图的执行过程
知识点
9. 某几何体的三视图如图所示,则该几何体外接球的表面积为 ( )
正确答案
解析
画出直观图,如图所示,几何体的外接球即为对应的棱长为1,1,2的长方体的外接球,所以2R=

考查方向
解题思路
借助长方体作出几何体的三视图如图所示,几何体的外接球,就是正方体的外接球,可直接算出球的表面积。
易错点
容易将几何体的三视图画错。
知识点
6. 在区间



正确答案
解析
命题“





考查方向
解题思路
由命题为真命题,可得
易错点
容易将区域画错
知识点
2.已知复数


正确答案
解析
z=

考查方向
解题思路
先作除法,后求模
易错点
除法化简易出错
知识点
5. 





正确答案
解析
由抛物线方程可知,准线方程为x=-










考查方向
解题思路
首先求抛物线的准线方程,再由抛物线的定义,过A,B向准线作垂线段, 再设A,B两点到y轴的距离为





易错点
抛物线的性质, 数学结合的应用.
知识点
8. 若函数




正确答案
解析
f(x)=cos2x-cos(2x+










考查方向
解题思路
先将原函数进行化简整理,f(x)= 


易错点
本小题易在平移过程中出错,忽略x系数2.
知识点
10. 若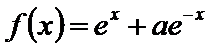
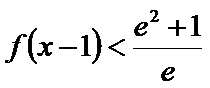
正确答案
解析
若f(x)=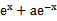
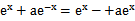
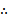
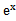
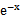
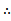
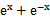
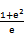
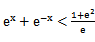
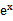
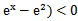
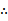
考查方向
解题思路
先由偶函数性质,求出a=1,将不等式进行化简整理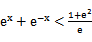
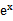
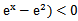
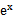
易错点
不等式的化简整理
知识点
11. 已知双曲线





正确答案
解析
如图,易知A(





考查方向
解题思路
画出简图,得出A(



易错点
不能利用双曲线的性质找到a,b,c系的关系
知识点
12. 设






正确答案
见解析
解析
画出[-1,3]函数的图象,如图所示,再利用周期将图象向左右复制,得到整个定义域内的图象,g(x)=f(x)-kx有且仅有五个零点,即y=f(x)与y=kx的图象有且仅有五个交点,当直线y=kx与第3段抛物线







考查方向
解题思路
首先画出分段函数,结合周期画出定义域内函数图像,图像是由一段抛物线(无左端点,有右端点)与一段折线(无左端点,有右端点)组成,并且区间长度为4,且f(x+4)=f(x), 说明函数周期为4, 所以整个定义域内的图像可以由基本图像进行复制, 如图所示, 不妨设从y轴右侧起,每段抛物线分别记为













易错点
函数零点的确定,数形结合,推理论证能力
知识点
13.已知




正确答案
解析
当x







考查方向
解题思路
求出x

易错点
不能正确求出x
知识点
14. 已知


正确答案
2
解析
画出可行域,如图,根据目标函数的斜率为

考查方向
解题思路
画出可行域,根据图形解出目标函数的最大值
易错点
可行域画错,目标函数的处理有误。
知识点
15.在正方形





正确答案
[4,8-2
解析
设CN=x,CM=y,

因为

















考查方向
解题思路
画出正方形,设CN=x,CM=y,将

易错点
处理变量之间的整体关系及转化
知识点
16. 设








正确答案
解析
f(
























考查方向
解题思路
可利用倒序相加求
易错点
求

知识点
已知向量

17.若

18.在




正确答案
解析

得
即


考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-



易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由

∴







考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
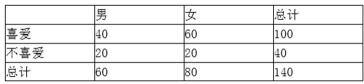
周立波是海派清口创始人和《壹周·立波秀》节目的主持人,他的点评视角独特,语言幽默犀利,给观众留下了深刻的印象.某机构为了了解观众对《壹周·立波秀》节目的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
19.从这60名男观众中按对《壹周·立波秀》节目是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
20,根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关.(精确到0.001)
21.从19题中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱《壹周·立波秀》节目的概率.
正确答案
喜爱的观众有4名;不喜爱的观众有2名.
解析
抽样比为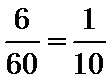
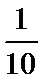
考查方向
解题思路
直接计算抽样比,即可算出喜爱与不喜爱的人数;
易错点
对“独立性检验的思想”不理解易出错
正确答案
不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
解析
假设:观众性别与喜爱无关,由已知数据可求得,
∴ 不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
考查方向
解题思路
直接代入公式计算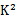
易错点
对“独立性检验的思想”不理解易出错
正确答案
0.4
解析
记喜爱的4名男性观众为a,b,c,d,不喜爱的2名男性观众为1
其中选到的两名观众都喜爱的事件有6个,
故其概率为
考查方向
解题思路
直接列出总事件及发生事件的情况,直接求比。
易错点
对“独立性检验的思想”不理解易出错
如图,在三棱柱




22.求证:

23.当三棱锥


正确答案
(略)
解析
连结















考查方向
解题思路
关键是在面DCB1中找线,连结


易错点
确定“三棱锥
正确答案
解析
设点








由(Ⅰ)知:




∵




∵




















考查方向
解题思路
当三棱锥





易错点
确定“三棱锥
已知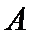
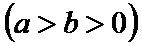
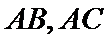
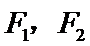
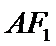
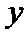
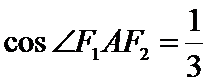
24.求该椭圆的离心率;
25.设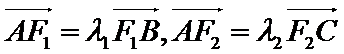
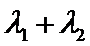
正确答案
.e=
解析
当线段A
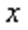
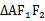
因为cos∠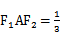
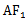
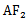
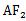

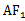

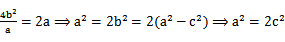
考查方向
解题思路
先证出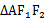
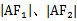
易错点
解析几何易出现对于直线方程的分类讨论上的错,其次就是直线与曲线联系以后,寻求向量、坐标、常数、参数之间的联系时,易出现转化和计算、代数整理上的错误。
正确答案
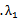

解析
由24得椭圆方程为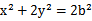

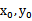

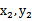
则直线AC的方程为y=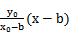
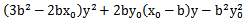
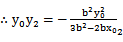


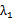
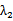
(2) 若AB⊥x轴,则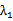
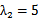
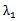
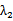
综上所述,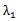
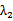
考查方向
解题思路
由24得到含有b的椭圆方程,根据题意对直线AB、AC的斜率进行分为讨论,设出坐标,联立方程组,利用根与系数关系,结合向量关系式,将向量关系转化为坐标关系,用A的坐标及b,表求
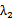
易错点
解析几何易出现对于直线方程的分类讨论上的错,其次就是直线与曲线联系以后,寻求向量、坐标、常数、参数之间的联系时,易出现转化和计算、代数整理上的错误。
选修4-1: 几何证明选讲.
如图所示,已知










28.求证:
29.若

正确答案
证明略
解析
∵



又∵


∴


又∵
考查方向
解题思路
先证明

易错点
找不准三角形相似或全等的条件
正确答案
PA=
解析
∵






∴


∴

考查方向
解题思路
先综合题中条件及28题中结论,解出EP=

易错点
找不准三角形相似或全等的条件
已知函数
26.若函数


27.若斜率为






正确答案

解析



因为函数




解得
考查方向
解题思路
直接求导,


易错点
函数的恒成立问题,构造新函数;用导数解决函数的综合性问题
正确答案
证明略
解析
设点



要证
即证










即

考查方向
解题思路
设出交点坐标,用分析法证明,要证



易错点
函数的恒成立问题,构造新函数;用导数解决函数的综合性问题