- 真题试卷
- 模拟试卷
- 预测试卷
4. 将函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
５．对某校400名学生的体重（单位：Ｋｇ）进行统计，得到如图所示的频率分布直方图，则学生体重在60以上的人数为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．设变量x，y满足约束条件
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．设集合
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8.用a，b，c表示三条不同的直线，γ表示平面，给出下列命题：
①若a∥b，b∥c，则a∥c；
②若a⊥b，b⊥c，则a⊥c；
③若a∥γ，b∥γ，则a∥b；
④若a⊥γ，b⊥γ，则a∥b.
其中真命题的序号是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2.等差数列
A1
B
C
D3
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1.集合
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3.已知向量
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．若一个底面为正三角形的几何体的三视图如图所示，则这个几何体的体积为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11.甲、乙两名篮球运动员在某几场比赛得分的茎叶图如图所示，则甲、乙两人这几场比赛得分的中位数之和是 （ ）
正确答案
64
解析
解析已在路上飞奔，马上就到！
知识点
14.在区间
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．在等差数列
正确答案
52
解析
解析已在路上飞奔，马上就到！
知识点
15.已知
正确答案
4
解析
解析已在路上飞奔，马上就到！
知识点
16．对一个边长为1的正方形进行如下操作：第一步，将它分割成3×3方格，接着用中心和四个角的5个小正方形，构成如图①所示的几何图形，其面积S1=
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．某地区有小学21所，中学14所，大学7所，现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
（1）求应从小学、中学、大学中分别抽取的学校数目。
（2）若从抽取的6所学校中随机抽取2所学校做进一步数据分析，
（i）列出所有可能的抽取结果；（ii）求抽取的2所学校均为小学的概率。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19． 已知在
（1）求角B的大小；
（2）若角B为锐角，
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18.如图，在三棱柱
（1）求证：
（2）若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20.已知递增等比数列
（Ⅰ）求数列
（Ⅱ）设数列
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21．某商场销售某种商品的经验表明，该商品每日的销售量
（Ⅱ） 若该商品的成本为3元/千克, 试确定销售价格
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
22．已知在平面直角坐标系xOy中的一个椭圆，它的中心在原点，左焦点为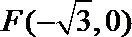
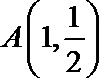
（1）求该椭圆的标准方程；
（2）过原点O的直线交椭圆于点B，C，求△ABC面积的最大值。
正确答案
解析
解析已在路上飞奔，马上就到！