• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
  • 教师招募
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
文科数学 文昌市2015年高三试卷
精品
|
立即下载

文科数学 热门试卷

X 查看更多试卷
试卷目录
1、单选题
1
2
3
4
5
6
7
8
9
10
11
12
2、填空题
13
14
15
16
3、简答题
17
18
19
20
21
22
  • 真题试卷
  • 模拟试卷
  • 预测试卷
查看更多 >
单选题 本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。
1
题型： 单选题
|
分值: 5分

1．集合，则（       ）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

并集及其运算
1
题型： 单选题
|
分值: 5分

8．平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则此球的体积为（       ）

Aπ

B6π

C4π

D4π

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

多面体和旋转体表面上的最短距离问题
1
题型： 单选题
|
分值: 5分

4．函数在处导数存在，若：；：是的极值点则（       ）

A是的充分必要条件

B是的充分条件，但不是的必要条件

C是的必要条件，但不是 的充分条件

D既不是的充分条件，也不是的必要条件

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定
1
题型： 单选题
|
分值: 5分

6．设 则（       ）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

对数值大小的比较
1
题型： 单选题
|
分值: 5分

2．复数（       ）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

复数代数形式的乘除运算
1
题型： 单选题
|
分值: 5分

5．的内角A、B、C的对边分别为a、b、c，若a、b、c成等比数列，且，则（       ）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

余弦定理
1
题型： 单选题
|
分值: 5分

9．一空间几何体的三视图如图所示,则该几何体的体积为（       ）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征
1
题型： 单选题
|
分值: 5分

10．执行如图所示的程序框图，则输出的k的值是（       ）

A3

B4

C5

D6

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

程序框图
1
题型： 单选题
|
分值: 5分

3．已知向量，,,则（       ）

A

B

C5

D25

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

向量的模平面向量数量积的运算
1
题型： 单选题
|
分值: 5分

7．已知ω>0，0<φ<π，直线和是函数f（x）=sin（ωx+φ）图像的两条相邻的对称轴，则φ=（       ）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的图象
1
题型： 单选题
|
分值: 5分

11．设F为抛物线的焦点，过F且倾斜角为的直线交于C于两点，则=（       ）

A

B12

C6

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的标准方程和几何性质抛物线焦点弦的性质
1
题型： 单选题
|
分值: 5分

12．函数在上单调，则a的取值范围是（       ）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点
填空题 本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。
1
题型：填空题
|
分值: 5分

15．设x，y满足的约束条件，则的最大值为__________。

正确答案

7

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质
1
题型：填空题
|
分值: 5分

14．设不等式组  ，表示平面区域为D，在区域D内随机取一个点，则此点到坐标原点的距离大于2的概率是__________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

与长度、角度有关的几何概型
1
题型：填空题
|
分值: 5分

13．函数在区间上的最大值是__________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域三角函数中的恒等变换应用三角函数的最值
1
题型：填空题
|
分值: 5分

16．在等差数列中，，公差为，前项和为，当且仅当时取最大值，则的取值范围__________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值
简答题（综合题） 本大题共70分。简答应写出文字说明、证明过程或演算步骤。
1
题型：简答题
|
分值: 12分

20． 已知椭圆C：+=1（a＞b＞0）的一个顶点为A（2,0），离心率为，直线与椭圆C交与不同的两点M,N

（1）求椭圆C的方程

（2）当△AMN的面积为时，求k的值.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题
1
题型：简答题
|
分值: 12分

21．已知函数的图象在与轴交点处的切线方程是。

（I）求函数的解析式；

（II）设函数，若的极值存在，求实数的取值范围以及函数取得极值时对应的自变量的值.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数研究函数的单调性利用导数求函数的极值利用导数求参数的取值范围
1
题型：简答题
|
分值: 12分

17．在等比数列{an}中，a2＝3，a5＝81.

（1） 求an；

（2） 设bn＝log3an，求数列{bn}的前n项和Sn。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用
1
题型：简答题
|
分值: 12分

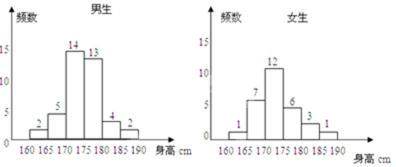
18．为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行分层抽样调查，测得身高情况的统计图如下：

（1）估计该校男生的人数；

（2）估计该校学生身高在170～185cm之间的概率；

（3） 从样本中身高在180～190cm之间的男生中任选2人，求至少有1人身高在185～190cm之间的概率。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

古典概型的概率分层抽样方法频率分布直方图
1
题型：简答题
|
分值: 10分

选做题：请在第22、23、24题中任选一题做答.

22．如图，已知AB是的直径，C、D是上两点，CE⊥AB于E，BD交AC于G，交CE于F，CF＝FG.

（1）求证：C是弧BD的中点；

（2）求证：BF＝FG.

23．已知曲线的极坐标方程为，曲线的极坐标方程为，曲线、相交于A、B两点．

（1）把曲线、的极坐标方程转化为直角坐标方程；

（2）求弦AB的长度. 

24．已知函数；

（1）若不等式的解集为，求实数的值；

（2）在（1）的条件下，若对一切实数x恒成立，求实数m的取值范围.

22．如图，已知AB是⊙O的直径，C、D是⊙O上两点，CE⊥AB于E，BD交AC于G，交CE于F，CF＝FG.

（1） 求证：C是弧BD的中点；

（2） 求证：BF＝FG.

23．已知曲线C1的极坐标方程为ρ＝6cosθ，曲线C2的极坐标方程为θ＝（ρ∈R），曲线C1、C2相交于A、B两点．

（1） 把曲线C1、C2的极坐标方程转化为直角坐标方程；

（2） 求弦AB的长度.

24．已知函数－

（1） 若不等式≤3的解集为-1≤≤，求实数的值；

（2） 在（1）的条件下，若≥对一切实数恒成立，求实数的取值范围.

第(1)小题正确答案及相关解析

正确答案

第(2)小题正确答案及相关解析

正确答案

第(3)小题正确答案及相关解析

正确答案

1
题型：简答题
|
分值: 12分

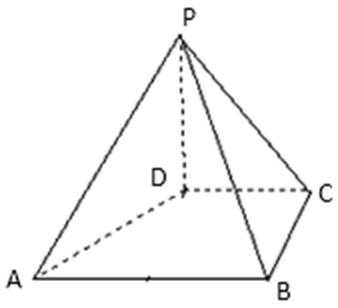
19． 如图，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=90°。

（1）求证：PC⊥BC；

（2）求点A到平面PBC的距离。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间中直线与直线之间的位置关系

点击 “立即下载”

即可下载本试卷，含解析哦

知道啦