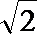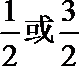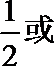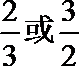- 真题试卷
- 模拟试卷
- 预测试卷
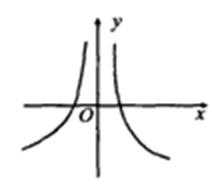
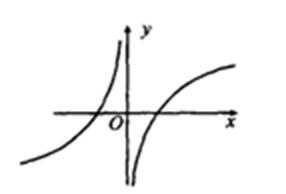
5．函数
A向右平移
B向右平移
C向左平移
D向左平移
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知等差数列{an}的公差d不为0，等比数列{bn}的公比q是小于1的正有理数。若a1=d，b1=d2，且
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．方程
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．已知空间直角坐标系
A
B
C3
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．复数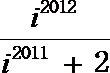
A
B
C―
D―
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．下图是一个算法的程序框图，该算法所输出的结果是 （ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．函数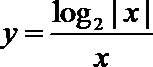
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．已知平面向量
A2
B3
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．根据下列三视图（如下图所示），则它的体积是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．设集合
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知x，y满足不等式组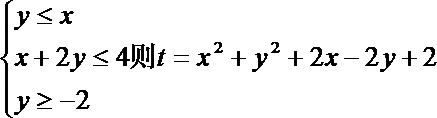
A
B2
C3
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．设圆锥曲线C的两个焦点分别为F1，F2，若曲线r上存在点P满足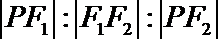
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．已知函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．一次选拔运动员，测得7名选手的身高（单位cm）分布茎叶图如图，
正确答案
6
解析
解析已在路上飞奔，马上就到！
知识点
15．在△ABC和△AEF中，B是EF的中点，AB=EF=1，BC=6，
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．下列说法：
①“
②函数
③命题“函数
④
其中正确的说法是_______.
正确答案
①④
解析
解析已在路上飞奔，马上就到！
知识点
19．一个四棱锥的三视图如图所示，E为侧棱PC上一动点。
（1）画出该四棱锥的直观图，并指出几何体的主要特征（高、底等）．
（2）点
正确答案
（1）直观图如下：
该四棱锥底面为菱形，边长为2，其中角A为60度，
顶点A在底面内的射影为底面菱形的中心，四棱锥高为1。
（2）当E为PC中点时，
如图所示：
证明：连接AC，且
∴O为AC的中点，又E为中点，∴OE为△ACP的中位线，
∴
当E为棱PC中点时， 
∴ＢＤ
同时
在
即
解析
解析已在路上飞奔，马上就到！
知识点
17．已知向量
（1）求
（2）求函数
正确答案
解析：（1）∵ 
∴ 
∴ 0≤
（2）∵ 
∴ 
∵ 
∴ 当
解析
解析已在路上飞奔，马上就到！
知识点
18．已知等差数列
（Ⅰ）求
（Ⅱ）令bn=
正确答案
解：（Ⅰ）设等差数列
因为
解得
（Ⅱ）由（Ⅰ）知
所以
即数列
解析
解析已在路上飞奔，马上就到！
知识点
20．某校高三年级共有450名学生参加英语口语测试，其中男生250名，女生200名。现按性别用分层抽样的方法从中抽取45名学生的成绩。
（I）求抽取的男生与女生的人数？
（II）从男生和女生中抽查的结果分别如下表1和表2；
分别估计男生和女生的平均分数，并估计这450名学生的平均分数。（精确到0．01）
正确答案
解：（Ⅰ）由抽样方法知，被抽取的男生人数为250×＝25，
被抽取的女生人数为200×＝20．
（Ⅱ）男生甲和女生乙被抽到的概率均为0.1，
所以男生甲与女生乙至少有1人被抽到的概率：P＝1－（1－0．1）2＝0.19．
（Ⅲ）由（Ⅰ）知，m＝25－（3＋8＋6）＝8，n＝20－（2＋5＋5）＝8，
据此估计 男生平均分为＝82.8，女生平均分为＝83；
这450名学生的平均分数为≈82.33．
解析
解析已在路上飞奔，马上就到！
知识点
21．椭圆
（１）求椭圆
（２）若直线
正确答案
解：（1） 
当
（2） 设
若
直线
解析
解析已在路上飞奔，马上就到！
知识点
22．设函数
（1）试求a、b的值；
（2）若
正确答案
解析：（1）
又
由①②得
又
∴
则x1、x2是方程
∴x1+x2=
∴
又∵x1≠x2，∴b= x1+x2=
（2）
由
由
则由
（或构造函数
综上，所求
解析
解析已在路上飞奔，马上就到！