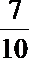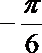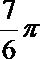- 真题试卷
- 模拟试卷
- 预测试卷
4.若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
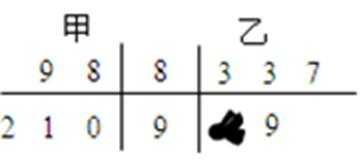
7.如图所示的茎叶图表示甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.某程序框图如图所示,若使输出的结果不大于 37,则输入的整数i的最大值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图所示,等边△ABC的边长为2,D为AC中点,且△ADE也是等边三角形,在△ADE以点A为中心向下转动到稳定位置的过程中,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合A={

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.为了得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若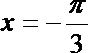
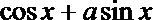
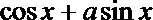
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.用C(A)表示非空集合A中的元素个数,定义A*B=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知直线l过点



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数





①函数
②函数
函数;
③如果当


最大值是4;
④当

⑤函数
其中正确命题的序号是
正确答案
②⑤
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数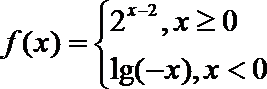
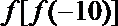

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形。
(1)求证:平面DEC⊥平面BDE;
(2)求二面角C—BE—D的余弦值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列


(1)求证:
(2)记


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量
(1)求
(2)将函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列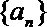

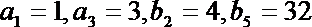
(1)求数列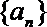
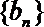
(2)设数列

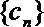
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.从标有1,2,3,…,7的7个小球中取出一个球,记下它上面的数字,放回后再取出一个球,记下它上面的数字,然后把两球上的数字相加,求取出两球上的数字之和大于11或者能被4整除的概率。
正确答案
从标有1,2,3,…,7的7个小球中取出一个球,记下它上面的数字,放回后再取出一个球,记下它上面的数字,共有7×7=49种不同情况,
其中两球上的数字之和大于11或者能被4整除的事件有:
(1,3),(1,7),(2,2),(2,6),(3,1),(3,5),(4,4),(5,3),
(5,7),(6,2),(6,6),(7,1),(7,5),(6,7),(7,6),(7,7),共16种,
故取出两球上的数字之和大于11或者能被4整除的概率P=
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数

(1)若

(2)若

正确答案
解析
解析已在路上飞奔,马上就到!