- 真题试卷
- 模拟试卷
- 预测试卷
2.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 一个几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.定义在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.阅读程序框图,若输入


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.下列说法中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设曲线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数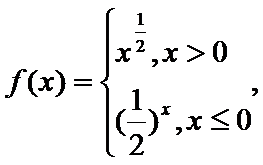
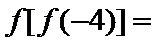
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
11.已知向量



正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
14.已知二次函数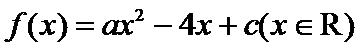
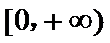
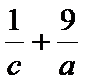
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
13. 在数列


正确答案
- 1
解析
解析已在路上飞奔,马上就到!
知识点
15.已知












①
②
③
④
则在区间

正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,在三棱柱






(Ⅰ)求证:

(Ⅱ)设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某小区在一次对20岁以上居民节能意识的问卷调查中,随机抽取了100份问卷进行统计,得到相关的数据如下表:
(Ⅰ)由表中数据直观分析,节能意识强弱是否与人的年龄有关?
(Ⅱ)据了解到,全小区节能意识强的人共有350人,估计这350人中,年龄大于50岁的有多少人?
(Ⅲ)按年龄分层抽样,从节能意识强的居民中抽5人,再从这5人中任取2人,求恰有1人年龄在20至50岁的概率.
正确答案
解:(Ⅰ)因为20至50岁的54人有9人节能意识强,大于50岁的46人有36人节能意识强,

(Ⅱ)年龄大于50岁的有
(Ⅲ)抽取节能意识强的5人中,年龄在20至50岁的
年龄大于50岁的4人,记这5人分别为A,B1,B2,B3,B4。
从这5人中任取2人,共有10种不同取法,完全正确列举,设A表示随机事件“这5人中任取2人,恰有1人年龄在20至50岁”,则A中的基本事件有4种:完全正确列举,故所求概率为
解析
解析已在路上飞奔,马上就到!
知识点
16.设


(Ⅰ)求
(Ⅱ)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知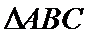
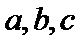
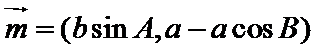
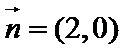
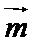
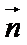
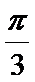
(Ⅰ)求角B的大小;
(Ⅱ)求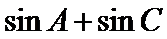
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知
(Ⅰ)当

(Ⅱ)当


(Ⅲ)若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(Ⅰ)求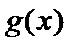
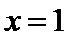
(Ⅱ)求
(Ⅲ)若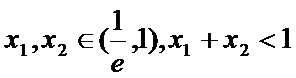
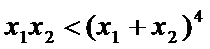
正确答案
解析
解析已在路上飞奔,马上就到!










































