- 真题试卷
- 模拟试卷
- 预测试卷
1.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知平面向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.命题“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知某几何体的侧视图与其正视图相同,相关的尺寸如下图所示,则这个几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知A、B两点分别在两条互相垂直的直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知各项为正的等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知幂函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知集合




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.定义运算


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在空间直角坐标系中,点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知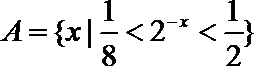
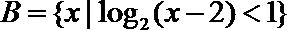
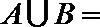
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知方程




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在如图的表格中,每格填上一个数字后,使得每一横行成等差数列,每一纵列成等比数列,则
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
16.四棱锥ABCD中,E、H分别是AB、AD的中点,F、G分别是CB、CD的中点,若AC+BD=3,AC·BD=1,则EG2+FH2=________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在工程技术中,常用到双曲正弦函数

正确答案
填入



解析
解析已在路上飞奔,马上就到!
知识点
19.在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1
(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(2)求直线EC与平面ABED所成角的正弦值
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知



(1)若外接圆O的半径
(2)求



正确答案
(1)由正弦定理有
∴


且B为钝角,∴
∴
又

(2)由已知

即
同理

两式相减得
即

解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(1)求函数
(2)若

正确答案
(1)已知函数即
∴ 
令
则
即函数

(2)由已知
∴ 当

解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列


(1)求

(2)设

正确答案
(1)由已知
即
∴
又
即
∴
(2)当

即

∴

∴


∴
∴

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)当

(2)若


(3)设函数







正确答案
(1)当


令





即函数的极大值为1,极小值为
(2)
若

则

若
若

若



解析
解析已在路上飞奔,马上就到!