- 真题试卷
- 模拟试卷
- 预测试卷
2.
正确答案
解析

知识点
5.已知向量



正确答案
解析





知识点
7.如果

正确答案
解析

知识点
1.已知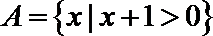
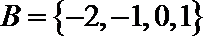
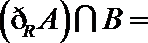
正确答案
解析
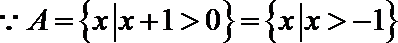
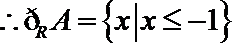
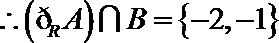
知识点
3.设




正确答案
解析
试题分析:方面,“非







知识点
8.已知




正确答案
解析





















故选C.
知识点
9.下列说法,正确的是( )
正确答案
解析
函数





























知识点
10.设












正确答案
解析
令
















知识点
6.函数
正确答案
解析







知识点
4.函数
正确答案
解析
自变量





知识点
17.已知函数
(1)求
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20..已知函数
(1)当

(2)求函数

(3)试证明:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设数列



(1)求


(2)已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求常数c的值;
(2)解不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设函数


终边经过点
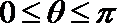
(1)若点
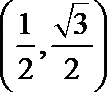

(2)若点
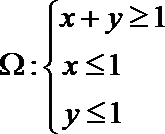
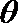

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19..设函数




(1)当


(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在




正确答案
解析
由正弦定理的




知识点
12.如果等差数列


正确答案
解析


知识点
13.已知函数

①图象

②图象

③函数

④由


其中正确的说法的序号为____________。
正确答案
②③
解析







当



将函数



综上所述,正确的命题序号是②③.
知识点
14.已知函数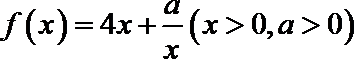
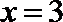
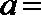
正确答案
解析
当