- 真题试卷
- 模拟试卷
- 预测试卷
2.设集合A=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.下列函数中,既是周期为π的周期函数又是偶函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.某公司2005~2010年的年利润x(单位:百万元)与年广告支出y(单位:百万元)的统计资料如下表所示:
根据统计资料,则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设命题p:∀x∈R,|x|≥x;q:∃x∈R,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.定义


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在极坐标系中,A(1,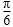
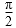
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设平面向量a=(1,2),b=(-2,y),若a∥b,则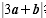
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.一空间几何体的三视图(单位:cm)如图所示,则此几何体的体积是___________cm3.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.直线l:x-y=0与椭圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.直线l: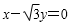
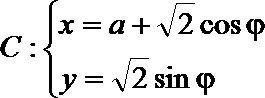
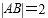
正确答案
2;ρ2-4ρcosθ+2=0
解析
解析已在路上飞奔,马上就到!
知识点
12.若{an}为等差数列,Sn是其前n项和.且S11=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f″(x)是函数y=f(x)的导数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点为函数y=f(x)的“拐点”。有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,求:
(1)函数f(x)=x3-3x2+3x对称中心为___________;
(2)若函数

正确答案
(1,1) ; 2010
解析
解析已在路上飞奔,马上就到!
知识点
17.如图:在矩形ABCD中,AB=5,BC=3,沿对角线BD把△ABD折起,使A移到A1点,过点A1作A1O⊥平面BCD,垂足O恰好落在CD上。
(1)求证:BC⊥A1D;
(2)求直线A1B与平面BCD所成角的正弦值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.工厂生产某种产品,次品率p与日产量x(万件)间的关系为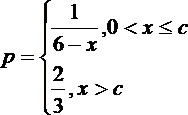
(1)将日盈利额y(万元)表示为日产量(万件)的函数;
(2)为使日盈利额最大,日产量应为多少万件?(注:次品率=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知f(x)=mx(m为常数,m>0且m≠1).设f(a1),f(a2),…,f(an)…(n∈N*)是首项为m2,公比为m的等比数列。
(1)求证:数列{an}是等差数列;
(2)若bn=an·f(an),且数列{bn}的前n项和为Sn,当m=2时,求Sn;
(3)若cn=f(an)lgf(an),问是否存在m,使得数列{cn}中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,请说明理由。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数f(x)=asinx+bcos(x-



(1)求实数a,b的值;
(2)求函数f(x)在[0,π]上的单调递增区间。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知动圆G过点F(

(1)求曲线E的方程;
(2)已知
(3)已知线段AB的垂直平分线交x轴于点C,其中x1≠x2且x1+x2=4.求△ABC面积的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!