- 真题试卷
- 模拟试卷
- 预测试卷
3.如图,在一个正方体内放入两个半径不相等的球





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知直线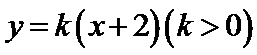

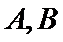
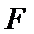
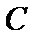
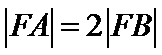

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若直线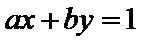
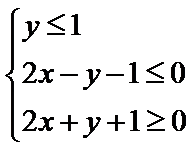
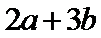
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.一束光线从点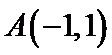
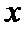
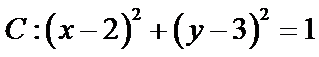
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在平面直角坐标系








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数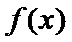
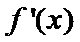

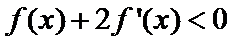
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.给出下列关于互不相同的直线

①
②
③
④
其中真命题是_____________(填序号)
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
11.已知数列



正确答案
2n-10
解析
解析已在路上飞奔,马上就到!
知识点
13.已知线段






正确答案
k≤-5或k≥1
解析
解析已在路上飞奔,马上就到!
知识点
14.已知圆

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.定义在区间







①
②
③
④
其中在区间
正确答案
①①
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,







(1)求证:
(2)设


(3)设平面


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知





(1)求数列
(2)若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求函数
(2)求函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知:以点





(1)求证:
(2)设直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆





(1)求椭圆C的方程;
(2)设椭圆










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1) 求函数
(2) 若函数






(3) 求证:
正确答案
解析
解析已在路上飞奔,马上就到!