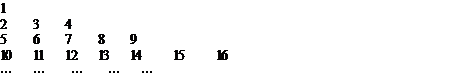- 真题试卷
- 模拟试卷
- 预测试卷
1.命题“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.“

正确答案
充分不必要
解析
解析已在路上飞奔,马上就到!
知识点
3.已知向量
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
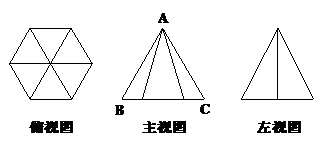
4.一个几何体的三视图如图所示,其中主视图中△ABC是边长为2的正三角形,俯视图为正六边形,那么该几何体的体积为________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知等差数列

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
9.已知实数x,y满足条件

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.将正整数排成下表,则数表中的2008出现在第_______行。
正确答案
45
解析
解析已在路上飞奔,马上就到!
知识点
13.第29届奥运会在北京举行.设数列an=

正确答案
2026
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.函数f(x)=|x2-a|在区间[-1,1]上的最大值为M(a),则M(a)的最小值是__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量

(1)求

(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.甲、乙两大超市同时开业,第一年的全年销售额均为a万元,由于经营方式不同,甲超市前n年的总销售额为

(1)设甲、乙两超市第n年的销售额分别为an, bn, 求an, bn的表达式;
(2)若其中某一超市的年销售额不足另一超市的年销售额的50%,则该超市将被另一超市收购,判断哪一超市有可能被收购?如果有这种情况,将会出现在第几年。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设P:关于


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,

(1)求证:AE⊥BE;
(2)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN//平面DAE。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知函数
(1)求
(2)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设函数f(x)的定义域为R,当x<0时,0<f (x)<1,且对任意的实数x, y∈R,有f(x+y)=f (x)f (y);
(1)求f (0), 并证明:当x∈R时, f (x)>0;
(2)判断并证明函数f (x)在R上的单调性;
(3)设数列{an}各项都是正数,且满足a1=f (0), f(an+12-an2)=


正确答案
解析
解析已在路上飞奔,马上就到!