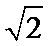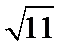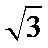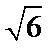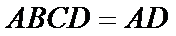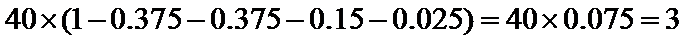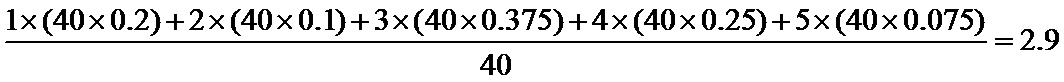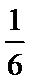- 真题试卷
- 模拟试卷
- 预测试卷
4.向量


正确答案
解析
由










考查方向
解题思路
先根据题意得到

易错点
不会根据

知识点
5.各项为正的等比数列




正确答案
解析
由




考查方向
解题思路
先根据题意得到

易错点
不知道

知识点
6.已知实数



正确答案
解析
做出可行域为三角形,最上边的交点的坐标为





考查方向
解题思路
1.先作出可行域; 2.在可行域中找到目标函数

易错点
1.可行域画错;
2.不知道目标函数
知识点
8.如右图所示的程序框图,若输出的
正确答案
解析








考查方向
解题思路
根据给出的程序框图循环执行,直到符合条件跳出循环。
易错点
无法确定程序结束的条件导致出错,误选B,D。
知识点
9.定义在





正确答案
解析
由
















考查方向
解题思路
先根据题中给出的信息判断出函数
易错点
不会将题中给出的条件转化到图像中,导致信息多而且混乱。
知识点
1.设集合A={x|x2﹣2x﹣3<0},B={x|y=lnx},则A∩B=( )
正确答案
解析


考查方向
解题思路
先求出集合A,B,然后利用数轴求出
易错点
对于集合B不理解其表示什么
知识点
2.已知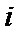
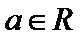
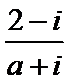

正确答案
解析
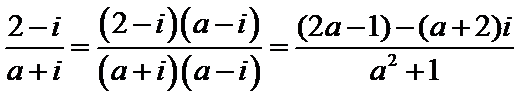
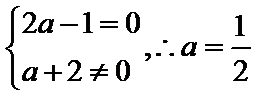
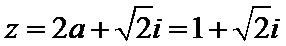
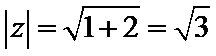
考查方向
解题思路
先利用复数的除法将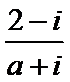
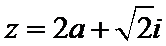
易错点
不知道纯虚数是什么导致出错。
知识点
7.一个几何体的三视图如图所示,且其侧(左)视图是一个等边三角形,则这个几何体的体积为( )
正确答案
解析
由三视图可知该几何体为一个三棱锥和一个四棱锥的组合体,其中高均为

考查方向
解题思路
1、将几何体放到长方体中考虑;
2、得到原来的几何体后求出其体积即可。
易错点
1.无法根据三视图还原成直观图;
2.不会计算得到几何体的体积。
知识点
10.已知点






正确答案
解析
由







考查方向
解题思路
1.先根据题中给出的条件求出
易错点
1.不会利用椭圆的定义这一隐含条件解决问题;
2.不能从题中给出的条件
知识点
3.
正确答案
解析
由





考查方向
解题思路
先根据题中条件判断出
易错点
由

12.一矩形的一边在


正确答案
解析
设矩形与函数

矩形绕





考查方向
解题思路
1.先根据题意确定

易错点
对于函数

知识点
11.函数

正确答案
解析





考查方向
解题思路
1.根据图像看出差别后带入解析式求证即可。
易错点
不会判断函数
知识点
15. 已知点








正确答案
解析
由题意得:












考查方向
解题思路
1.先将题中给出的信息表示出来,在三角形中,利用三角函数的定义表示出
2.然后利用角
易错点
1.不会利用定义转化题中的条件
2.不知道该用什么知识建立关于a,b,c之间的等量关系。
知识点
13.记集合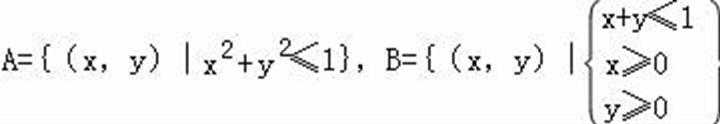
正确答案
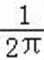
解析
由题意知,集合A表示的平面区域为以原点为圆心,1为半径的圆,其面积为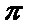
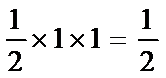
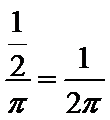
考查方向
解题思路
先求出集合A,B表示平面区域的面积,然后利用几何概型的概率公式求解即可。
易错点
不理解题中给出的条件是让求什么
知识点
14.已知

正确答案
解析
由




考查方向
解题思路
先将题中给出的等式化简,得到

易错点
在利用三角函数公式化简时出错。
知识点
16.数列




正确答案
15
解析


考查方向
解题思路
先化简数列
易错点
不知道数列
知识点
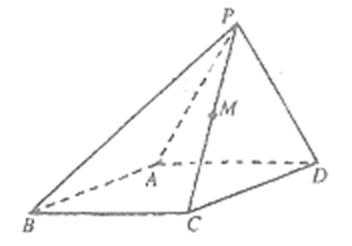
如图,四棱锥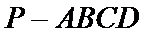
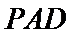
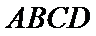
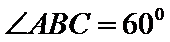
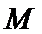
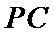
22.求证: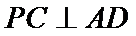
23.求点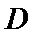
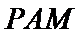
正确答案
(1)略;
解析
(1):取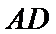
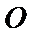
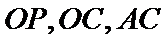
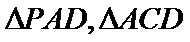
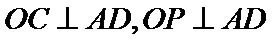
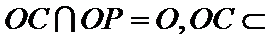
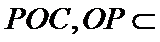
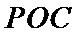
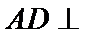
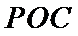
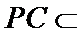
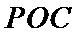
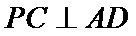
考查方向
解题思路
先证明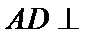
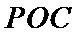
易错点
不会做辅助线导致没有思路;
正确答案
(2)
解析
(2)点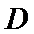
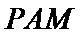
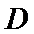
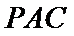
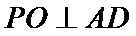
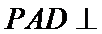
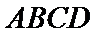
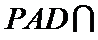

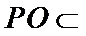
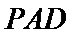
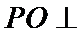
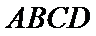
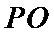
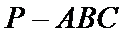
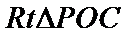
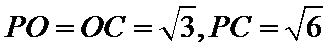
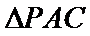
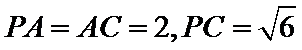
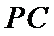
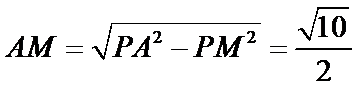
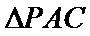
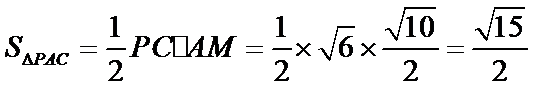
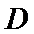
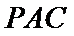
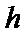
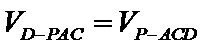
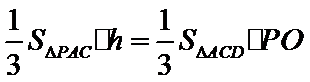
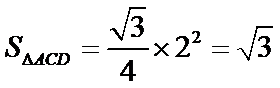
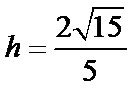
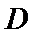
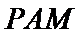
考查方向
解题思路
先发现点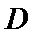
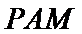
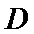
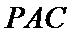
易错点
看不出点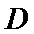
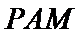
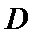
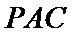
如图,在平面直角坐标系





24.若


25.若直线


正确答案
(1)
解析
(1)由圆









联立①②,解得


考查方向
解题思路
先根据题中条件求出圆心的坐标,后即可得到圆
易错点
不知题中给出的直线
正确答案
(2)
解析
(2)因为直线








即

考查方向
解题思路
根据直线和圆相切得


易错点
不会化简


已知函数
17.当

18.若




正确答案
(1)
解析
(1)



考查方向
解题思路
1。第(1)问先化简函数为一个角的一个三角函数,然后求其值域;
易错点
1.第(1)问直接将区间的端点带入函数导致值域出错;
正确答案
(2)
解析
(2)∵由题意可得

化简可得:





考查方向
解题思路
2.先由


易错点
2.第(2)问
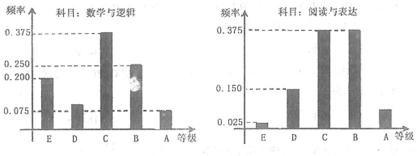
在某大学自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分别为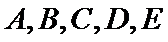
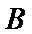
19.求该考场考生中“阅读与表达”科目中成绩为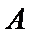
20.若等级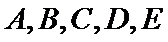
21.已知参加本考场测试的考生中,恰有两人的两科成绩均为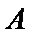
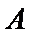
正确答案
(1)3;
解析
(1)因为“数学与逻辑”科目中成绩等级为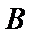
所以该考场有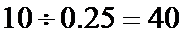
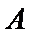
考查方向
解题思路
先根据频率分布直方图求出第(1)问;
易错点
对于题中给出的信息不理解或理解错误;
正确答案
解析
(2)该考场
考查方向
解题思路
根据第(1)问的结果估和频率分布直方图估计该考场考生“数学与逻辑”科目的平均分;
易错点
不会根据频率分布直方图估计平均值。
正确答案
(3)
解析
(3)因为两科考试中,共有6人得分等级为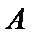
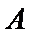
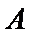

考查方向
解题思路
按照古典概型求概率的过程求解即可。
易错点
对于题中给出的信息不理解或理解错误
已知











28.求
29.若

正确答案
(1)
解析
(1)∵







又

考查方向
解题思路
先根据弦切角定理得


易错点
没有发现
正确答案
(2)
解析
(2)∵,∴





考查方向
解题思路
先证明
易错点
看不出
已知函数
26.若曲线



27.若


正确答案
(1)



解析
(1) 由已知得

而



则

那么






由


考查方向
解题思路
直接利用求导,导数的几何意义直接得到所求的切线方程;后得到
易错点
求函数的单调区间时不注意定义域出错;
正确答案
(2)
解析
(2)若

即

设












从而实数
考查方向
解题思路
先分离参数后,构造函数
易错点
不会分离参数,构造函数导致无从下手。