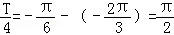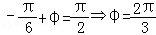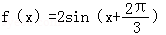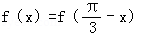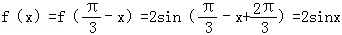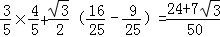- 真题试卷
- 模拟试卷
- 预测试卷
7.已知某几何体的三视图如图所示,则这个几何体的外接球的表面积等于( )
正确答案
解析
略。
知识点
2.设复数z的共轭复数为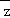
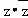
正确答案
解析
略。
知识点
8.已知m,n是满足m+n=1,且使

正确答案
解析
略。
知识点
9.对于实数m,n定义运算“⊕”:m⊕n=
正确答案
解析
略。
知识点
4.以下判断正确的是( )
正确答案
解析
略。
知识点
5.若直线l1:2x+(m+1)y+4=0与直线l2:mx+3y﹣2=0平行,则m的值为( )
正确答案
解析
略。
知识点
10.对于一个有限数列p=(p1,p2,…,pn),p的蔡查罗和(蔡查罗是一位数学家)定义为
正确答案
解析
略。
知识点
1.设全集I=R,集合A={y|y=log2x,x>2},B={x|y=
正确答案
解析
略。
知识点
3.如图是某体育比赛现场上七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
正确答案
解析
略。
知识点
6.某程序框图如图所示,若输出的S=120,则判断框内为( )
正确答案
解析
略。
知识点
11.平面向量





正确答案
2
解析
略。
知识点
14.若不存在实数x使|x﹣3|+|x+1|≤a成立,则实数a的取值范围是________。
正确答案
(-∞,4)
解析
略。
知识点
15.在区间[0,1]上随意选择两个实数x,y,则使
正确答案
解析
略。
知识点
13.设双曲线


正确答案
解析
略。
知识点
16.观察下列等式:
①sin2θ=cosθ•2sinθ
②sin4θ=cosθ(4sinθ﹣8sin3θ)
③sin6θ=cosθ(6sinθ﹣32sin3θ+32sin5θ)
④sin8θ=cosθ(8sinθ﹣80sin3θ+192sin5θ﹣128sin7θ)
⑤sin10θ=cosθ(10sinθ﹣160sin3θ+msin5θ﹣1024sin7θ+nsin9θ)
则可以推测(1)n=________;(2)m=________。
正确答案
(1)n=512
(2)m=672
解析
略。
知识点
17.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f′′(x)是f′(x)的导数,若方程f′′(x)有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数f(x)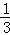
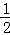

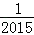
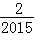

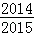
正确答案
2014
解析
略。
知识点
12.设x,y满足约束条件
正确答案
29
解析
略。
知识点
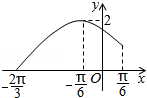
18.定义在区间[﹣
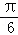
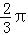

(1)求函数y=f(x)的表达式;
(2)设θ∈[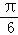
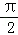

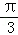
正确答案
(1)f(x)=
(2)
解析
(1)当 x∈[﹣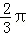
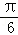
∴T=2π,故ω=1
又f(x)=Asin(ωx+φ)过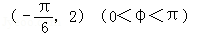
∴
∴
∵函数y=f (x)的图象关于直线
∴
当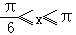
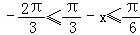
∴
∴f(x)=
(2)∵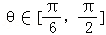
∴由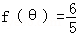
因此,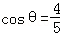
∴
=
知识点
19.数列{an}中,已知a1=1,n≥2时,an=
(1)求证:数列{bn}是等差数列;
(2)求数列{an}的前n项和Sn。
正确答案
见解析。
解析
(1)证明:由
得:
∴
即bn=bn﹣1+2⇒bn﹣bn﹣1=2(n≥2)
又
∴数列{bn}是首项为2,公差为2的等差数列。
(2)解:由(1)知,bn=2+(n﹣1)×2=2n,
∴
记
则
两式相减得:
=
∴
因此,
知识点
20.如图,四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=
(1)证明:AA1⊥BD
(2)证明:平面A1BD∥平面CD1B1;
(3)求三棱柱ABD﹣A1B1D1的体积。
正确答案
见解析。
解析
(1)证明:∵底面ABCD是正方形,
∴BD⊥AC,
又∵A1O⊥平面ABCD且BD⊂面ABCD,
∴A1O⊥BD,
又∵A1O∩AC=O,A1O⊂面A1AC,AC⊂面A1AC,
∴BD⊥面A1AC,AA1⊂面A1AC,
∴AA1⊥BD
(2)∵A1B1∥AB,AB∥CD,
∴A1B1∥CD,
又A1B1=CD,
∴四边形A1B1CD是平行四边形,
∴A1D∥B1C,同理A1B∥CD1,
∵A1B⊂平面A1BD,A1D⊂平面A1BD,CD1⊂平面CD1B1,B1C⊂平面CD1B,
且A1B∩A1D=A1,CD1∩B1C=C,
∴平面A1BD∥平面CD1B1
(3)∵A1O⊥面ABCD,
∴A1O是三棱柱A1B1D1﹣ABD的高,
在正方形ABCD中,AO=1.
在Rt△A1OA中,AA1=2,AO=1,
∴A1O=
∴V三棱柱ABD﹣A1B1D1=S△ABD•A1O=


∴三棱柱ABD﹣A1B1D1的体积为
知识点
21.已知函数f(x)=x2﹣mlnx,h(x)=x2﹣ax+1(a>0)
(1)设A是函数f(x)=x2﹣mlnx上的定点,且f(x)在A点的切线与y轴垂直,求m的值;
(2)讨论f(x)的单调性;
(3)若存在实数m使函数f(x),h(x)在公共定义域上具有相同的单调性,求证:m≥﹣
正确答案
见解析。
解析
(1)由题意得:A(1,1),
又f′(x)=2x﹣
∵f(x)在A点的切线与y轴垂直,
∴f′(1)=0,∴2﹣m=0,∴m=2;
(2)∵f′(x)=2x﹣

∴若m≤0则f(x)在(0,+∞)单调递增,
若m>0,由f′(x)>0,可得x>

由f′(x)<0可得0<x<
∴m>0时,f(x)的递增区间是(

综上可得:m≤0时,f(x)增区间为(0,+∞),无减区间,
m>0时,f(x)的递增区间是(

(3)易知f(x),h(x)的公共定域为(0,+∞),
∵在(0,+∞)上,h(x)的递增区间是(

∴若存在实数m使函数f(x),h(x)在公共定域上具有相同的单调性,
再由(2)可得m=0且


令g(a)=m+

则g(a)=


∴g′(a)=a2+a﹣6,(a>0),
由g′(a)>0,解得:a<﹣3,(舍),或a>2,
由g′(a)<0,解得:0<a<2,
∴g(a)在(0,2)递减,在(2,+∞)递增;
∴g(a)min=f(2)=

∴g(a)≥g(2)=0,即m≥﹣
知识点
22.已知椭圆E:



(1)求椭圆E的方程;
(2)已知点M(2,1),斜率为
①若直线l过椭圆的左顶点,求k1,k2的值;
②试猜测k1,k2的关系,并给出你的证明。
正确答案
见解析。
解析
(1)设椭圆的右焦点(c,0),
由右焦点到直线y=x的距离为

又由椭圆的离心率为
∴

∴椭圆E的方程为
(2) ①若直线l过椭圆的左顶点,则直线的方程是
联立方程组

故
②设在y轴上的截距为b,∴直线l的方程为y=
由
设A(x1,y1),B(x2,y2),
则x1+x2═﹣2b,x1x2=2b2﹣4
又

故k1+k2=

又

所以上式分子=
=x1x2+(b﹣2)(x1+x2)﹣4(b﹣1)=2b2﹣4+(b﹣2)(﹣2b)﹣4(b﹣1)=0,
故k1+k2=0