- 真题试卷
- 模拟试卷
- 预测试卷
3.执行如图所示的程序框图,输出的s值为
正确答案
解析
由程序框图得k=o s=0 k=1 s=1 k=2 s=9 k=3不满足
考查方向
解题思路
按程序框图的流程顺序一步一步进行计算,直到
易错点
计算时需注意
知识点
6.从甲、乙等5名学生中随机选出2人,则甲被选中的概率为
正确答案
解析
设5个人分别为a b c d e
(a , b) (a , c) (a , d) (a , e) (b , c) (b , d) (b , e) (c , d) (c , e) (d , e)
含a的情况有: (a , b) (a , c) (a , d) (a , e) 所以a被选中的概率为:
考查方向
解题思路
分析题中所有情况的种数,以及含a的种数,利用古典概型的概率公式进行计算
易错点
分清该题为取球问题的一起取情况
知识点
7.已知A(2,5),B(4,1).若点P(x,y)在线段AB上,则2x−y的最大值为
正确答案
解析
由线性规划的知识可知,在(4,1)处2x-y取得最大值为7 在(2,5)处2x-y取得最小值为-1
考查方向
解题思路
可以画图利用线性规划的知识计算
易错点
分清在在(4,1)处2x-y取得最大值 在(2,5)处2x-y取得最小值
知识点
1.已知集合
正确答案
解析
考查方向
解题思路
利用数轴把集合画出来,并找集合A与集合B的公共部分
易错点
集合的端点分清取舍
知识点
2.复数
正确答案
解析
考查方向
解题思路
复数的除法,分子分母同时乘以分母的共轭复数,进而计算
易错点
计算过程中注意
知识点
4.下列函数中,在区间
正确答案
解析
画出每个函数的图像,由图像得d是对的
考查方向
解题思路
画出每个函数的图像
易错点


知识点
5.圆(x+1)2+y2=2的圆心到直线y=x+3的距离为
正确答案
解析
圆心(-1,0) 直线为x-y+3=0 由点到线的距离公式得:
考查方向
解题思路
由题意得圆心,利用点到线距离公式计算
易错点
注意圆心的坐标符号
知识点
8.某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
正确答案
解析
由题意得立定跳远决赛的有8人,所以序号为1,2,3,4,5,6,7,8的学生入选,又因为同时进入立定跳远决赛和30秒跳绳决赛的有6人,所以30秒跳绳决赛的6人一定从1~8学号的学生选取,假设5号不入选,那么1~8序号的学生中有5人入选,与题意6人入选矛盾,所以5号一定入选。
考查方向
解题思路
把成绩由高到低排列,分析入选情况
易错点
分清9.10一定不入选,再假设分析前8个入选情况
知识点
9.已知向量
正确答案
解析

考查方向
解题思路
利用向量夹角公式进行计算
易错点
要选用向量夹角的坐标公式
知识点
10.函数
正确答案
2
解析
画出
由图像可知当
所以x=2时,y取得最大值为2
考查方向
解题思路
画图分析单调性得最值
易错点
函数的图像
知识点
11.某四棱柱的三视图如图所示,则该四棱柱的体积为___________.
正确答案
解析
由题意得
考查方向
解题思路
由已知三视图分析底面积与高 ,进而利用体积公式计算
易错点
分清底面积
知识点
12.已知双曲线

正确答案
1 2
解析
由题意渐近线方程为:


因为焦点为

考查方向
解题思路
利用双曲线的几何性质进行计算
易错点
渐近线为 
知识点
13.在△ABC中,


正确答案
1
解析
因为




考查方向
解题思路
应用正弦定理进行计算
易错点
已知正弦值求角
知识点
14.某网店统计了连续三天售出商品的种类情况:第一天售出19种商品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品有3种,后两天都售出的商品有4种,则该网店
①第一天售出但第二天未售出的商品有______种;
②这三天售出的商品最少有_______种.
正确答案
16 29
解析
(1)由题意第一天与第二天都售出的有3种 所以第一天售出但第二天未售出的商品有19-3=16
(2)当商品种数最少时,应让这三天售出相同的种数最多 (用不同的数字代表不同的商品)
第一天:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
第二天:1 2 3 4 21 22 23 24 25 26 27 28 29
第三天:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
所以这三天售出的商品中相同的商品种数为29种
考查方向
解题思路
让第一天与第三天出售相同的商品种数最多
易错点
分清第一天与第三天出售相同商品的种数
知识点
如图,在四棱锥P-ABCD中,PC⊥平面ABCD,
21.求证:
22.求证:
23.设点E为AB的中点,在棱PB上是否存在点F,使得
正确答案
(I)因为

所以
又因为
所以
考查方向
解题思路
(1)利用直线垂直平面的判定定理证明
(2)利用平面垂直平面的判定定理证明
(3)利用直线平行平面的判定分析
易错点
应用直线垂直平面的判定定理时,要注意直线垂直平面中的2条相交线
应用直线平行平面的判定定理时,要注意平面外一条直线平行面内一条直线
正确答案
因为

所以
因为

所以
所以

所以平面

考查方向
解题思路
(1)利用直线垂直平面的判定定理证明
(2)利用平面垂直平面的判定定理证明
(3)利用直线平行平面的判定分析
易错点
应用直线垂直平面的判定定理时,要注意直线垂直平面中的2条相交线
应用直线平行平面的判定定理时,要注意平面外一条直线平行面内一条直线
正确答案
棱



取




又因为

所以
又因为

所以

考查方向
解题思路
(1)利用直线垂直平面的判定定理证明
(2)利用平面垂直平面的判定定理证明
(3)利用直线平行平面的判定分析
易错点
应用直线垂直平面的判定定理时,要注意直线垂直平面中的2条相交线
应用直线平行平面的判定定理时,要注意平面外一条直线平行面内一条直线
设函数
26.求曲线

27.设

28.求证:

正确答案
由

因为

所以曲线


考查方向
解题思路
(1)利用导数的几何意义计算(2)利用极值与单调性计算
易错点
有三个零点时一定要检验
正确答案
当

所以
令






所以,当





由


考查方向
解题思路
(1)利用导数的几何意义计算(2)利用极值与单调性计算
易错点
有三个零点时一定要检验
正确答案
当


此时函数


当


当



当



所以
综上所述,若函数

故

当



所以

因此

考查方向
解题思路
(1)利用导数的几何意义计算(2)利用极值与单调性计算
易错点
有三个零点时一定要检验
已知{an}是等差数列,{bn}是等差数列,且b2=3,b3=9,a1=b1,a14=b4.
15.求{an}的通项公式;
16.设cn=an+bn,求数列{cn}的前n项和.
正确答案
(I)等比数列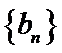
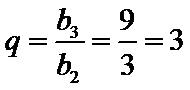
所以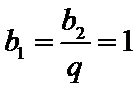
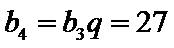
设等差数列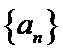
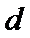
因为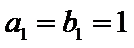
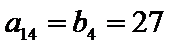
所以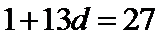
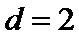
所以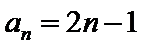
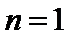
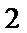
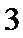
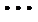
考查方向
解题思路
(1)利用数列的公式,列方程,解方程
(2)利用数列求和公式进行计算
易错点
分清等差数列与等比数列,应用相应公式计算
正确答案
由(I)知,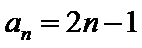
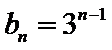
因此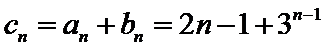
从而数列
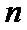
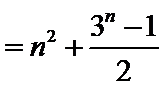
考查方向
解题思路
(1)利用数列的公式,列方程,解方程
(2)利用数列求和公式进行计算
易错点
分清等差数列与等比数列,应用相应公式计算
已知函数f(x)=2sin ωxcosωx+cos 2ωx(ω>0)的最小正周期为π.
17.求ω的值;
18.求f(x)的单调递增区间.
正确答案
(I)因为

所以

依题意,

考查方向
解题思路
(1)利用三角函数公式化简,进而利用周期公式求解
(2)利用三角函数的单调性计算
易错点
三角函数公式的化简
正确答案
由(I)知
函数


由
得
所以


考查方向
解题思路
(1)利用三角函数公式化简,进而利用周期公式求解
(2)利用三角函数的单调性计算
易错点
三角函数公式的化简
某市民用水拟实行阶梯水价,每人用水量中不超过w立方米的部分按4元/立方米收费,超出w立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
19.如果w为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,w至少定为多少?
20.假设同组中的每个数据用该组区间的右端点值代替,当w=3时,估计该市居民该月的人均水费.
正确答案
由用水量的频率分布直方图知,
该市居民该月用水量在区间




率依次为




所以该月用水量不超过



依题意,

考查方向
解题思路
利用频率分布直方图与平均数的知识计算
易错点
该题平均水费的运算量有些大,计算要细心
正确答案
由用水量的频率分布直方图及题意,得居民该月用水费用的数据分组与频率分布表:
组号
1
2
3
4
5
6
7
8
分组
频率
根据题意,该市居民该月的人均水费估计为:

考查方向
解题思路
利用频率分布直方图与平均数的知识计算
易错点
该题平均水费的运算量有些大,计算要细心
已知椭圆C:
24.求椭圆C的方程及离心率;
25.设P为第三象限内一点且在椭圆C上,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:四边形ABNM的面积为定值.
正确答案
由题意得,

所以椭圆

又
所以离心率
考查方向
解题思路
(1)由椭圆的几何性质公式进行计算
(2)将点设为
易错点
四边形的面积的计算,注意式子的正负
正确答案
设



又

直线

令


直线

令


所以四边形

从而四边形
考查方向
解题思路
(1)由椭圆的几何性质公式进行计算
(2)将点设为
易错点
四边形的面积的计算,注意式子的正负