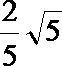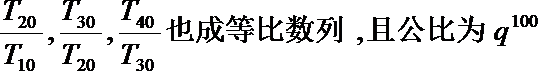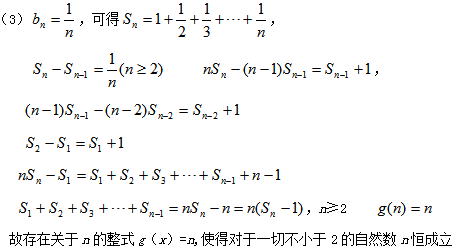- 真题试卷
- 模拟试卷
- 预测试卷
4.如图所示,墙上挂有一边长为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数z =i2(1+i)的虚部为__________。
正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
9.将一枚骰子抛掷两次,若先后出现的点数分别为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.将正奇数排列如下表其中第





正确答案
60
解析
解析已在路上飞奔,马上就到!
知识点
2.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若曲线
正确答案
(1,0)
解析
解析已在路上飞奔,马上就到!
知识点
6.若椭圆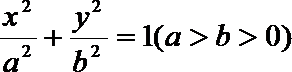
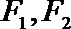
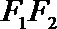
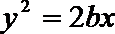
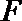
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.下面伪代码的输出结果为_________。
正确答案
26
解析
解析已在路上飞奔,马上就到!
知识点
8.公差为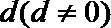
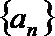


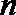

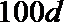

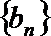

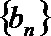
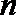
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知点O为


正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
13.对于函数



正确答案
0.5
解析
解析已在路上飞奔,马上就到!
知识点
14.三位同学合作学习,对问题“已知不等式


甲说:“可视

乙说:“不等式两边同除以
丙说:“把字母
参考上述思路,或自已的其它解法,可求出实数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在一个密封的容积为1的透明正方体容器内装有部分液体,如果任意转动该正方体,液面的形状都不可能是三角形,那么液体体积的取值范围是________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数f(x)=x2-x+alnx
(1)当


(2)讨论
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列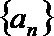
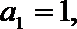
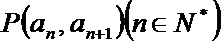
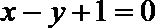
(1)求数列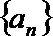
(2)若函数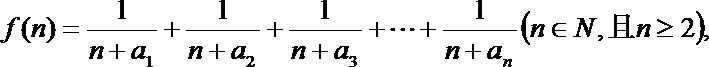
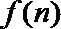
(3)设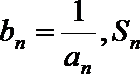
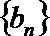
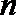
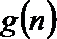
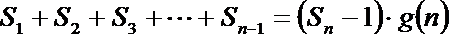
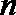
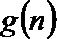
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)当

(2)设|MN|=

(3)在(2)的条件下,若对任意的正整数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知向量a=(sin(

(1)求f(x)的最小正周期和单调增区间;
(2)如果三角形ABC中,满足f(A)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数

(1)设


(2)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.即将开工的上海与周边城市的城际列车铁路线将大大缓解交通的压力,加速城市之间的流通。根据测算,如果一列火车每次拖4节车厢,每天能来回16次;如果每次拖7节车厢,则每天能来回10次。每天来回次数是每次拖挂车厢个数的一次函数,每节车厢一次能载客110人,试问每次应拖挂多少节车厢才能使每天营运人数最多?并求出每天最多的营运人数。(注:营运人数指火车运送的人数)
正确答案
解析
解析已在路上飞奔,马上就到!