- 真题试卷
- 模拟试卷
- 预测试卷
2.设集合

正确答案
解析
由数轴表示可得:
考查方向
解题思路
直接画数轴,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在判断端点时发生错误。
知识点
8.三棱锥
正确答案
解析
由图可知,PC=4,AC=4,B到AC的距离为2√3,解得BC=4,则PB=
考查方向
解题思路
1、还原几何体,表示对应的边长;
2、求出PB,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在还原几何体时发生错误。
知识点
9.如果执行如右面的程序框图,那么输出的S=()
正确答案
解析
由题可知,T=1,S=1,k=2;T=2,S=5,k=3;T=6,S=23,k=4;T=24,S=119,k=5;T=120,S=719,k=6.
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
本题考查流程图,解题步骤如下:
1、由题可知,依次计算T,S的值。
2、注意k的取值变化.
易错点
本题易在T和S的顺序上发生错误。
知识点
1.i是虚数单位,复数
正确答案
解析

考查方向
解题思路
直接计算,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在求共轭复数时发生错误。
知识点
3.下列选项错误的是()
正确答案
考查方向
解题思路
本题考查简易逻辑的问题,解题步骤如下:
由题可知,若“
易错点
本题易在判断正误上发生错误。
知识点
4.使函数


正确答案
考查方向
解题思路
本题考查三角函数的图象与性质,解题步骤如下:
由题可知, 

故需要

A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在公式化简上发生错误。
知识点
5.已知平面向量


正确答案
考查方向
解题思路
本题考查平面向量的模的计算,解题步骤如下:
1、由题可知,易得
2、由
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在应用数量积的公式时发生错误。
知识点
7.已知双曲线


正确答案
解析
c2=5+m=9,解得m=4=b2,所以
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
本题考查双曲线的焦点位置及渐近线方程,解题步骤如下:
1、由题可知,易得x2的系数为负,y2系数为正。
2、c2=5+m=9,解得m=4.
易错点
本题易在求解时把分母平方运算。
知识点
1




正确答案
解析
当


考查方向
解题思路
1、在圆中表示出直线的位置;
2、利用圆的性质求解,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在表示长度时发生错误。
知识点
6.在正项等比数列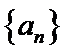
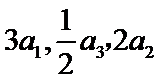
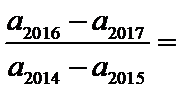
正确答案
解析
由题可知:a3=3a1+2a2,即a1q2=3a1+2a1q,解得q=-1(舍去)或q=2.a2016=a2014q2,
a2017=a2014q3,a2015=a2014q,约分即可。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
1、求出q;
2、代入计算,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在求q时发生错误。
知识点
11.函数

正确答案
a≥-1
解析
由图可知:a≥-1。
考查方向
解题思路
本题考查函数的图像性质,解题思路如下:
1、画出函数f(x)的图像及y=x的图像;
2、比较函数值的大小。
易错点
本题必须注意单调性的比较
知识点
14.若


正确答案
2.5
解析
由题可知,求出阴影区域的三个端点坐标,分别代入目标函数计算,即可求出最大值2.5
考查方向
解题思路
1、表示平面区域;
2、求出区域的端点坐标,即可得到结果。
易错点
本题易在表示平面区域时发生错误。
知识点
12.某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末位数记为x,那么x的值为________
正确答案
2
解析
由题可知,(180+181+171+172+174+175+170+x)/5=175,解得:x=2
考查方向
解题思路
本题考查统计的知识,解题思路如下:利用平均数的计算求出x即可
易错点
本题必须注意茎叶图的读数规则
知识点
13.锐角三角形ABC中,


正确答案
(√2,√3)
解析
由题可知,sinB=sin2A,B=2A∈(0o,90o),所以A∈(0o,45o), C=180O-A-B∈(0o,90o), 所以A∈(30o,45o)。b/a=sinB/sinA=2cosA∈(√2,√3)
考查方向
解题思路
本题考查解三角形的知识,解题思路如下:利用角度的范围及正弦定理计算即可
易错点
本题必须注意锐角三角形内角的范围
知识点
15.已知函数



正确答案
5
解析
由题可知:f(1)+f(2)+f[f(1)]=4, 且
f(2)+f(3)+f[f(2)]=7,故f(3)=4;f(3)+f(4)+f[f(3)]=10,故f(4)=3;
f(4)+f(5)+f[f(4)]=13,故f(5)=6;
f(5)+f(6)+f[f(5)]=16,则 f(6)=5。
考查方向
解题思路
本题考查函数的性质,解题思路如下:反复代值计算即可
易错点
本题必须注意反复代值计算
知识点
16. 

(I)求函数
(II)若


正确答案
(1)4;(2)
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难.
①
所以f(x)的最大值为4.
②因为f(x)=1,所以


所以

考查方向
解题思路
本题考查三角函数问题,解题步骤如下:
1、利用数量积公式及两角和差公式化简求最值。
2、利用两角和差公式求解。
易错点
注意角度的范围,忽视则容易出错。
知识点
17. 学业水平考试后,某校对高二学生的数学、英语成绩进行了统计,结果如图表所示(人数):已知英语、数学的优秀率分别为24%、30%(注:合格人数中不包含优秀人数).
(I)求a、b的值;
(II)现按照英语成绩的等级,采用分层抽样的方
正确答案
(1)20,30;(2)
解析
试题分析:本题属于概率统计中的基本问题,题目的难度是逐渐由易到难.
①设该校高二学生共有x人,已知英语优秀的有70+30+20=120人,依题意得:
120/x=0.24,解得:x=500,(70+60+a)/500=0.3,解得:a=20,从而b=30.
②由题意知,抽取的数学不合格的6 人中,英语优秀的应取2 人,分别记为a1 ,a 2,
英语合格的应取3人,分别记为 b1,b2 ,b3 ,英语不合格的应取1人,记为c .从中任取2人的结果一共有15种,其中,英语成绩恰为一人优秀一人合格的有6种。所以P=6/15=2/5。
考查方向
解题思路
本题考查概率统计,解题步骤如下:
1、利用频数分布表的数据求解。
2、写出基本事件的内容,并求出相应的概率。
易错点
1、第一问中的优秀率的计算。
2、第二问中基本事件对应的概率。
知识点
18. 四棱锥



(I)若平面


(II)求证:
正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
证明:(Ⅰ) 因为 AD// BC , AD 

所以BC //平面PAD
又平面PBC 过BC ,且与平面PAD 交于l。所以 l // BC
(Ⅱ)连结BD,△ABD中,
AD =a, AB =2a,∠DAB = 60 ,由余弦定理:
BD2 =DA2+AB2 -2DA×ABcos60O , 解得BD =3a
因为AB2 =AD2 +BD2所以△ABD为直角三角形,BD ⊥AD
因为 AD// BC,所以BC ⊥BD.又因为PD ⊥平面 ABCD,所以BC ⊥PD
因为PD∩ BD =D,所以BC ⊥平面PBD。平面BC在平面PBC内,
所以:平面PBD⊥平面PBC.又因为Q为中点 ,所以DQ⊥PB
所以:DQ⊥面PBC。PC 属于平面PBC。所以DQ ⊥PC
考查方向
解题思路
本题考查立体几何中的线面位置关系,解题步骤如下:
1、利用线面平行的性质定理。
2、利用线面垂直的定义及判定定理转化。
易错点
1、第一问中的线线平行的判定。
2、第二问中求证线面垂直时要与平面内的两条相交直线垂直。
知识点
19. 设数列




(I)求数列

(II)将数列






正确答案
(1)
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
(1)由已知得
(2)由已知得:

首项分别是

T2006=(c1+c3+……+c2015)+(c2+……+c2016)=
考查方向
解题思路
本题考查数列问题,解题步骤如下:
1、利用an与Sn的关系求解。
2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
21

(I)若

(II)若当

(III)若
正确答案
(1)f(x)在(-∞,-1)和(0,+∞)上单调递增,在(-1,0)上单调递减;
(2)a≤1;(3)a=1
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)要注意对参数的讨论.
(1)令f’(x)=ex-1+xex-x=(ex-1)(x+1)>0,得x<-1或x>0.
所以:f(x)在(-∞,-1)和(0,+∞)上单调递增,在(-1,0)上单调递减。
(2)f(x)=x(ex-1-ax),令g(x)= ex-1-ax,则g’(x)= ex-a.
若a≤1,则当x>0时g’(x)>0,g(x)为增函数,而g(0)=0,从而当x≥0时f(x)≥0;
若a>1,则当x∈(0,lna)时,g’(x)<0, g(x)为减函数,而g(0)=0,从而当x∈(0,lna)时,g(x)<0,即f(x)<0。
综上得a≤1.
(3)若f(x)无极值,则f(x)在R上单调。由f’(x)=(x+1)ex-1 -2ax,
若f(x)在R上单调递减,则f’(x)≤0,而利用不等式ex≥1+x,得f’(x)>0,与假设矛盾。
因此,f(x)在R上单调递增,即f’(x)≥0,显然f’(0)=0。
①当x>0时,2a≤

下面证明h(x)在(-∞,0)上单调递增:

当x>0时r’(x)>0,r(x)为增函数,r(x)>r(0)=0,h’(x)>0,h(x)在(0,+∞)上单调递增;
当x<0时r’(x)<0,r(x)为减函数,r(x)>r(0)=0,h’(x)>0,h(x)在(-∞,0)上单调递增;
当x>0时,由ex>1+x,得
得:2a≤2,a≤1。
②当x<0时,2a≥g(x),此时
得:2a≥2,a≥1。
综上得:a=1时f(x)无极值。
考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
本题考查导数的性质,解题步骤如下:
1、求导,然后解导数不等式,求单调区间。
2、对参数分类讨论求得零点个数。
易错点
第二问中的易丢对a的分类讨论。
知识点
20. 如图所示的封闭曲线C由曲线





(I)求曲线
(II)若点Q是曲线

(III)若点F为曲线



正确答案
(1)

解析
试题分析:本题属于圆锥曲线中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意对参数的讨论.
(1)
从而A(-2,0),所以C2的方程为x2+y2=4(y<0).
(2)由上可知:AB直线方程为:x-2y+2=0由题可知,当曲线C2在点Q的切线与AB平行时,
由直线与圆相切得:t=-2√5,或t=2√5(舍去)。此时
(3)由题可知:k≠0.
由

所以MF//PN
考查方向
解题思路
本题考查圆锥曲线与直线的位置关系,解题步骤如下:
1、利用e和c求a,b。
2、联立直线与椭圆方程求解。
易错点
第二问中的分类讨论。


















































