文科数学济南市2015年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．命题“若”是真命题，则下列命题一定是真命题的是（）

A若

B若

C若

D若

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定

题型：单选题

分值: 5分

3．“a=-1”是“直线与直线互相垂直”的（）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

5．已知=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：单选题

分值: 5分

10．已知函数是定义在R上的可导函数，其导函数记为，若对于任意实数x，有，且为奇函数，则不等式的解集为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

题型：单选题

分值: 5分

4．已知函数，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：单选题

分值: 5分

1．集合，，则等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

交集及其运算

题型：单选题

分值: 5分

6．设a＝，b＝，c＝，则a，b，c的大小关系是（）

Aa>c>b

Ba>b>c

Cc>a>b

Db>c>a

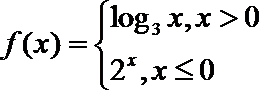
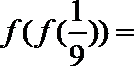
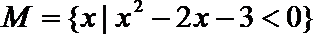
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数单调性的应用

题型：单选题

分值: 5分

7．设向量满足||=||=1，，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：单选题

分值: 5分

8．若∈（0，），且，则的值等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

9．下列函数中，在上为增函数的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

12．函数在点的切线方程为:_________

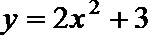
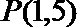
正确答案

4x-y+1=0

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：填空题

分值: 5分

13．在△ABC中，如果，那么等于_________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

诱导公式的推导

题型：填空题

分值: 5分

11．命题“对任意的，≤0”的否定为:__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的否定

题型：填空题

分值: 5分

14．函数对于任意实数满足条件，若，则=__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的单调性及单调区间

题型：填空题

分值: 5分

15．已知函数构造函数，定义如下:当时，;当时，．那么的最大值为_______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

19．在中，角的对边分别为，。

（1）求的值；

（2）求的面积．

正确答案

（1）

（2）

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 13分

20．已知函数

（1）若a＝－1，求f（x）的单调区间；

（2）若f（x）有最大值3，求a的值；

（3）若f（x）的值域是（0，＋∞），求a的取值范围。

正确答案

（1）当a＝－1时，f（x）＝，

令g（x）＝－x2－4x＋3，

由于g（x）在（－∞，－2）上单调递增，在（－2，＋∞）上单调递减，

而y＝t在R上单调递减，所以f（x）在（－∞，－2）上单调递减，在（－2，＋∞）上单调递增，

即函数f（x）的递增区间是（－2，＋∞），递减区间是（－∞，－2）．

（2）令h（x）＝ax2－4x＋3，y＝h（x），

由于f（x）有最大值3，所以h（x）应有最小值－1，因此，

解得a＝1．即当f（x）有最大值3时，a的值等于1．

（3）由指数函数的性质知，要使y＝h（x）的值域为（0，＋∞）．

应使h（x）＝ax2－4x＋3的值域为R，

因此只能有 a＝0．

因为若a≠0，则h（x）为二次函数，其值域不可能为R．故a的取值范围是a＝0．

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 14分

21．设。

（I）求的单调区间和最小值；

（II）讨论与的大小关系；

（III）求的取值范围，使得＜对任意＞0成立。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数单调性的应用

题型：简答题

分值: 12分

16．已知函数。

（1）的最小正周期；

（2）若，求的值域。

正确答案

（1）周期

（2）值域为：（1，]

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：简答题

分值: 12分

17．已知：、、是同一平面内的三个向量，其中＝（1，2）

（1）若||，且，求的坐标；

（2）若||=且与垂直，求与的夹角θ。

正确答案

（1）或

（2）

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 12分

18．已知命题P：函数y＝loga（1－2x）在定义域上单调递增；命题Q：不等式（a－2）x2＋2（a－2）x－4<0对任意实数x恒成立．若P∨Q是真命题，求实数a的取值范围

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷