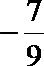- 真题试卷
- 模拟试卷
- 预测试卷
1． 已知集合U=R，集合
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．设x，y∈R，则“x≥2且y≥2”是“x2＋y2≥4”的( )
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．下列函数中，在区间
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．不等式
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．若平面向量
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．若
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．设O为坐标原点，
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．在等差数列
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．对一切实数x，不等式x2＋a|x|＋1≥0恒成立，则实数a的取值范围是( )
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．在△ABC中，角A，B，C所对的边长分别为a，b，c，若∠C＝120°，c＝a，则( )
A
B
C
Da与b的大小关系不能确定
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．已知sin(
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．给出下列四个结论：
①“若
②若
③函数
④对于任意实数x，有
其中正确结论的序号是___________.（填上所有正确结论的序号）
正确答案
④
解析
解析已在路上飞奔，马上就到！
知识点
14．函数f(x)＝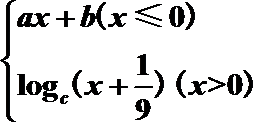
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．已知函数
正确答案
9
解析
解析已在路上飞奔，马上就到！
知识点
19．数列
（1）求
（2）是否存在等比数列
正确答案
（1）因为
即
所以
所以有
（2）存在.
由（1），
所以有
所以由 
所以存在以
其通项公式为
解析
解析已在路上飞奔，马上就到！
知识点
请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题计分。
22．选修4－1：平面几何证明选讲
如图，AB是⊙O的直径，点P在AB的延长线上，PC与⊙O相切于点C，PC＝AC＝1.
求⊙O的半径．
23．选修4－4：极坐标和参数方程
已知某条曲线C的参数方程为(其中t是参数，a∈R)，点M(5,4)在该曲线上。
（1）求常数a；
（2）求曲线C的普通方程．
24.选修4－5：不等式选讲
已知函数
（1）当
（2）若关于
正确答案
22.
23.
24．（１）
（２）
解析
解析已在路上飞奔，马上就到！
知识点
17．如图，为了计算衡水湖岸边两景点B与C的距离，由于地形的限制，需要在岸上选取A和D两个测量点，
现测得AD⊥CD，AD＝100m，AB＝140m，∠BDA＝60°，∠BCD＝135°，求两景点B与C之间的距离(假设A，B，C，D在同一平面内，测量结果保留整数；参考数据：
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．若向量
若函数
（1）求
（2）将函数
正确答案
（1）解：
由题意可知其周期为
（2）解：将
由其对称性，可设交点横坐标分别为
则
解析
解析已在路上飞奔，马上就到！
知识点
21．已知函数
（1）若
（2）求
（3）设
正确答案
（1）由已知
故曲线
（2）
①当
所以，
②当
在区间
所以，函数
（3）由已知，转化为
由（2）知，当
(或者举出反例：存在
当
故
所以
解得
解析
解析已在路上飞奔，马上就到！
知识点
20．已知函数
（1）求函数
（2）函数
正确答案
（1）
当
当
f(x)的单调递增区间为（
（2）
解析
解析已在路上飞奔，马上就到！