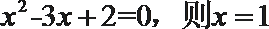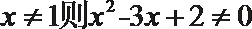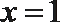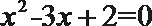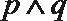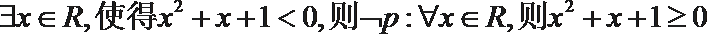文科数学湛江市2015年高三试卷

精品

单选题
简答题
填空题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、简答题

3、填空题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

6．以下有关命题的说法错误的是（）

A命题 “若”的逆否命题为“若

B“”是“”的充分不必要条件

C若为假命题，则p、q均为假命题

D对于命题p：

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

7．函数f（x）＝12x－x3在区间［－3，3］上的最小值是（）

A－9

B－16

C－12

D－11

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的最值

题型：单选题

分值: 5分

2．已知复数z＝，则z的实部为（）

C－2

D－1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

1. 若集合A＝{0，1，2，4}，B＝{1，2，3}，则A∩B＝（）

A{0，1，2，3，4}

B{0，4}

C{1，2}

D{3}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：单选题

分值: 5分

3．已知角的终边经过点(－4，3)，则＝（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的最值

题型：单选题

分值: 5分

4．下列函数中，既是偶函数又在区间(－∞，0)上单调递增的是（）

Af(x)＝

Bf(x)＝x2＋1

Cf(x)＝x3

Df(x)＝2－x

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明函数奇偶性的判断

题型：单选题

分值: 5分

8. 函数的单调递减区间是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值

题型：单选题

分值: 5分

9. 函数的部分图象是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：单选题

分值: 5分

10. 定义在上的函数满足：恒成立，若，则与的大小关系为（）

D的大小关系不确定

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

5. 等于（）

A－

B－

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

简答题（综合题）本大题共80分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

17.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图3，其中甲班学生的平均分是85，乙班学生成绩的中位数是83.

（1）求和的值；

（2）从成绩在90分以上的学生中随机抽取两名学生，求甲班至少有一名学生的概率.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

古典概型的概率茎叶图众数、中位数、平均数

题型：简答题

分值: 12分

16.已知

（1）求的值；

（2）求的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

同角三角函数间的基本关系两角和与差的余弦函数两角和与差的正弦函数二倍角的正弦

题型：简答题

分值: 14分

18.设函数，且.

（1）求的值及的定义域；

（2）求在区间上的值域。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数的运算性质对数函数的定义域对数函数的值域与最值

题型：简答题

分值: 14分

19.将函数的图像向左平移个得到偶函数的图像。

（1）求解析式；

（2）求的最大值及单调增区间。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的奇偶性正弦函数的单调性函数y=Asin（ωx+φ）的图象变换三角函数的最值

题型：简答题

分值: 14分

20．已知函数，且在时函数取得极值.

（Ⅰ）求的值及的极值；

（Ⅱ）若，证明：当时，的图象恒在的上方.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的极值利用导数求函数的最值利用导数证明不等式

题型：简答题

分值: 14分

21．已知函数

（1）求的单调区间；

（2）时，判断方程:根的个数并说明理由；

（3）有两个极值点且证明:.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数证明不等式

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

12.已知函数在区间上是减函数，则的取值范围是________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：填空题

分值: 5分

选做题：第14、15题是选做题，只能做1题，2题全答的，只计算前1题的得分．

14．（几何证明选讲）

如图2，为⊙的直径，，弦交于点．若，，则的长为______．

15.（坐标系与参数方程选讲）

若点在曲线（为参数，）上，则的取值范围是______．

正确答案

14. 1

15.

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：填空题

分值: 5分

13.如图1所示是函数y＝2sin(ωx＋φ) 的一段图象，则ω=____φ=______.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由y=Asin（ωx+φ）的部分图象确定其解析式

题型：填空题

分值: 5分

11.曲线在点(1,3)处的切线的方程是_________ .

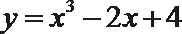
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷